
已知a>0,函数f(x)=-2asin(2x+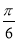 )+2a+b,当x∈[0,
)+2a+b,当x∈[0,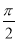 ]时,-5≤f(x)≤1.
]时,-5≤f(x)≤1.
(1)求常数a,b的值;
(2)设g(x)=f(x+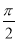 )且lg[g(x)]>0,求g(x)的单调区间.
)且lg[g(x)]>0,求g(x)的单调区间.
(1)a=2,b=-5
(2)综上,g(x)的递增区间为(kπ,kπ+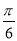 ](k∈Z);递减区间为(kπ+
](k∈Z);递减区间为(kπ+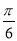 ,kπ+
,kπ+ )(k∈Z).
)(k∈Z).
【解析】【解析】
(1)∵x∈[0,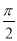 ],
],
∴2x+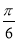 ∈[
∈[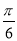 ,
,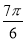 ].
].
∴sin(2x+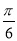 )∈[-
)∈[-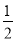 ,1],
,1],
又∵a>0,
∴-2asin(2x+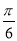 )∈[-2a,a].
)∈[-2a,a].
∴f(x)∈[b,3a+b],
又∵-5≤f(x)≤1,
∴b=-5,3a+b=1,
因此a=2,b=-5.
(2)由(1)得a=2,b=-5,
∴f(x)=-4sin(2x+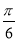 )-1,
)-1,
g(x)=f(x+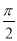 )=-4sin(2x+
)=-4sin(2x+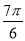 )-1=4sin(2x+
)-1=4sin(2x+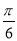 )-1,
)-1,
又由lg[g(x)]>0,得g(x)>1,
∴4sin(2x+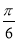 )-1>1,
)-1>1,
∴sin(2x+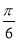 )>
)>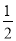 ,
,
∴2kπ+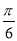 <2x+
<2x+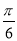 <2kπ+
<2kπ+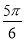 ,k∈Z,
,k∈Z,
其中当2kπ+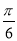 <2x+
<2x+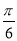 ≤2kπ+
≤2kπ+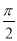 ,k∈Z时,g(x)单调递增,即kπ<x≤kπ+
,k∈Z时,g(x)单调递增,即kπ<x≤kπ+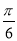 ,k∈Z,
,k∈Z,
∴g(x)的单调增区间为(kπ,kπ+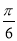 ],k∈Z.
],k∈Z.
又∵当2kπ+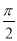 <2x+
<2x+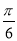 <2kπ+
<2kπ+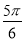 ,k∈Z时,g(x)单调递减,
,k∈Z时,g(x)单调递减,
即kπ+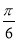 <x<kπ+
<x<kπ+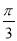 ,k∈Z.
,k∈Z.
∴g(x)的单调减区间为(kπ+ ,kπ+
,kπ+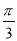 ),k∈Z.
),k∈Z.
综上,g(x)的递增区间为(kπ,kπ+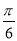 ](k∈Z);递减区间为(kπ+
](k∈Z);递减区间为(kπ+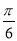 ,kπ+
,kπ+ )(k∈Z).
)(k∈Z).


科目:高中数学 来源:2015高考数学(理)一轮配套特训:3-8解三角形应用举例(解析版) 题型:选择题
如图,某海上缉私小分队驾驶缉私艇以40 km/h的速度由A处出发,沿北偏东60°方向进行海面巡逻,当航行半小时到达B处时,发现北偏西45°方向有一艘船C,若船C位于A的北偏东30°方向上,则缉私艇所在的B处与船C的距离是( )

A.5(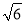 +
+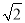 ) km B.5(
) km B.5(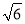 -
- ) km
) km
C.10( -
-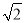 ) km D.10(
) km D.10( +
+ ) km
) km
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:3-5两角和与差的正弦、余弦和正切(解析版) 题型:解答题
已知α,β∈(0,π),且tanα=2,cosβ=- .
.
(1)求cos2α的值;
(2)求2α-β的值.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:3-4正弦型函数的图象及应用(解析版) 题型:填空题
函数f(x)=Asin(ωx+φ)(A>0,ω>0,0≤φ<2π)在R上的部分图象如图所示,则f(2014)的值为________.
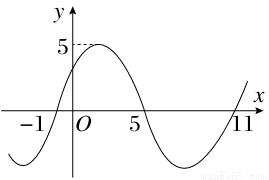
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:3-4正弦型函数的图象及应用(解析版) 题型:选择题
将函数f(x)=sin(2x+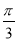 )的图象向左平移φ个单位,得到偶函数g(x)的图象,则φ的最小正值为( )
)的图象向左平移φ个单位,得到偶函数g(x)的图象,则φ的最小正值为( )
A.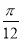 B.
B.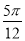 C.
C.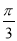 D.
D.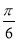
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:3-3三角函数的图象与性质(解析版) 题型:填空题
设函数f(x)=3sin(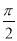 x+
x+ ),若存在这样的实数x1,x2,对任意的x∈R,都有f(x1)≤f(x)≤f(x2)成立,则|x1-x2|的最小值为________.
),若存在这样的实数x1,x2,对任意的x∈R,都有f(x1)≤f(x)≤f(x2)成立,则|x1-x2|的最小值为________.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:2-9函数模型及其应用(解析版) 题型:选择题
已知一容器中有A,B两种菌,且在任何时刻A,B两种菌的个数乘积为定值1010,为了简单起见,科学家用PA=lg(nA)来记录A菌个数的资料,其中nA为A菌的个数,则下列判断中正确的个数为( )
①PA≥1;
②若今天的PA值比昨天的PA值增加1,则今天的A菌个数比昨天的A菌个数多了10个;
③假设科学家将B菌的个数控制为5万个,则此时5<PA<5.5.
A.0 B.1 C.2 D.3
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:2-8函数与方程(解析版) 题型:选择题
已知x0是f(x)=(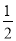 )x+
)x+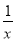 的一个零点,x1∈(-∞,x0),x2∈(x0,0),则( )
的一个零点,x1∈(-∞,x0),x2∈(x0,0),则( )
A.f(x1)<0,f(x2)<0 B.f(x1)>0,f(x2)>0
C.f(x1)>0,f(x2)<0 D.f(x1)<0,f(x2)>0
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:2-6对数与对数函数(解析版) 题型:选择题
设a=log3π,b=log2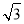 ,c=log3
,c=log3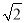 ,则( )
,则( )
A.a>b>c B.a>c>b C.b>a>c D.b>c>a
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com