练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】若S是公差不为0的等差数列的前项和，且成等比数列。

    (1)求等比数列的公比；

    (2)若，求的通项公式；

    (3)设， 是数列的前项和，求使得对所有都成立的最小正整数。

    【答案】(1) 4(2) (3) 30

    【解析】试题（1）本题考察的是求等比数列的公比，根据题目所给条件，利用等差数列和等比数列的通项公式即可求出等比数列的公比。

    （2）由（1）和，可得，所以即可解得，代入等差数列的通项公式即可得到的通项公式。

    （3）由（2）求得的通项，然后利用裂项相消求和法，求出，再利用放缩法和数列的单调性即可得到所求的的最大值。

    试题解析：因为数列为等差数列，所以，

    又成等比数列所以

    因为公差不等于0，所以

    （1）

    （2）因为

    （3）因为

    所以

    要对恒成立，则， 的最大值为19．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系中，一个动圆经过点且与直线相切，设该动圆圆心的轨迹为曲线.

    （1）求曲线的方程；

    （2）过点作直线交曲线于，两点，问曲线上是否存在一个定点，使得点在以为直径的圆上？若存在，求出点的坐标；若不存在，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某工厂生产某种型号的电视机零配件，为了预测今年月份该型号电视机零配件的市场需求量，以合理安排生产，工厂对本年度月份至月份该型号电视机零配件的销售量及销售单价进行了调查，销售单价（单位：元）和销售量（单位：千件）之间的组数据如下表所示：

    月份

    销售单价（元）

    销售量（千件）

    （1）根据1至月份的数据，求关于的线性回归方程（系数精确到）；

    （2）结合（1）中的线性回归方程，假设该型号电视机零配件的生产成本为每件元，那么工厂如何制定月份的销售单价，才能使该月利润达到最大（计算结果精确到）？

    参考公式：回归直线方程，其中.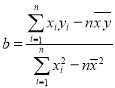

    参考数据：.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】每个国家对退休年龄都有不一样的规定，从2018年开始，我国关于延迟退休的话题一直在网上热议，为了了解市民对“延迟退休”的态度，现从某地市民中随机选取100人进行调查，调查情况如下表：

    年龄段（单位：岁）

    被调查的人数

    赞成的人数

    （1）从赞成“延迟退休”的人中任选1人，此人年龄在的概率为，求出表格中的值；

    （2）若从年龄在的参与调查的市民中按照是否赞成“延迟退休”进行分层抽样，从中抽取10人参与某项调查，然后再从这10人中随机抽取4人参加座谈会，记这4人中赞成“延迟退休”的人数为，求的分布列及数学期望.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示，椭圆，、，为椭圆的左、右顶点．

    设为椭圆的左焦点，证明:当且仅当椭圆上的点在椭圆的左、右顶点时，取得最小值与最大值．

    若椭圆上的点到焦点距离的最大值为，最小值为，求椭圆的标准方程．

    若直线与中所述椭圆相交于、两点（、不是左、右顶点），且满足，求证：直线过定点，并求出该定点的坐标．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知，不等式的解集是.

    （1）求的解析式；

    （2）不等式组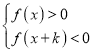的正整数解只有一个，求实数k取值范围；

    （3）若对于任意，不等式恒成立，求t的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设X～N(μ1，)，Y～N(μ2，)，这两个正态分布密度曲线如图所示，下列结论中正确的是 (　　)

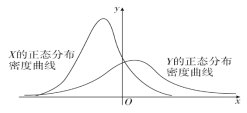
    A. P(Y≥μ2)≥P(Y≥μ1)

    B. P(X≤σ2)≤P(X≤σ1)

    C. 对任意正数t，P(X≥t)≥P(Y≥t)

    D. 对任意正数t，P(X≤t)≥P(Y≤t)

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知抛物线和点，直线与抛物线交于不同两点，，直线与抛物线交于另一点．给出以下判断：

    ①直线与直线的斜率乘积为；

    ②轴；

    ③以为直径的圆与抛物线准线相切.

    其中，所有正确判断的序号是（ ）

    A.①②③B.①②C.①③D.②③

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某车间为了规定工时额定，需要确定加工零件所花费的时间，为此作了次试验，得到数据如下：

    零件数/个

    10

    20

    30

    40

    50

    60

    加工时间/min

    64

    70

    77

    82

    90

    97

    （1）试对上述变量与的关系进行相关性检验，如果与具有线性相关关系，求出对的回归直线方程；

    （2）根据（1）的结论，你认为每小时加工零件的数量额定为多少（四舍五入为整数）比较合理？

    附：相关性检验的临界值表

    小概率

    0.05

    0.01

    3

    0.878

    0.959

    4

    0.811

    0.917

    5

    0.754

    0.874

    6

    0.707

    0.834

    ，

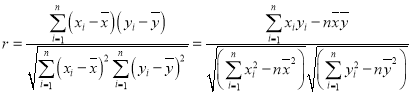
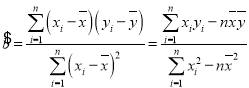    参考数据：；

    17950

    9100

    39158

    1750

    758

    查看答案和解析>>

    同步练习册答案