
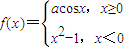 在x=0处连续,则a=-1;
在x=0处连续,则a=-1;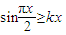 恒成立,则实数k的取值范围是[0,1];
恒成立,则实数k的取值范围是[0,1];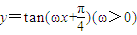 的图象按向量
的图象按向量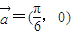 平移后,与函数
平移后,与函数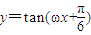 的图象重合,则ω的最小值为
的图象重合,则ω的最小值为 .
.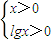 ,从而可判断①的正误;
,从而可判断①的正误;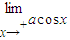 =a=
=a=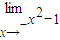 =-1,可判断②的正误;
=-1,可判断②的正误; ,k=
,k=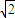 ,有
,有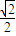 ≥
≥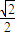 ,成立,从而可③的正判断误;
,成立,从而可③的正判断误; y=tan(ω(x-
y=tan(ω(x-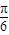 )+
)+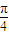 )=tan(ωx+
)=tan(ωx+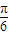 )?ω=
)?ω= -6k(k∈Z),由此可判断④的正误;
-6k(k∈Z),由此可判断④的正误; ?x>1,
?x>1,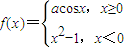 在x=0处连续,
在x=0处连续,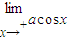 =a=
=a= =-1,
=-1, ,k=
,k=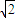 ,有
,有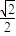 ≥
≥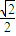 ,成立,故实数k的取值范围是[0,1]是错误的;
,成立,故实数k的取值范围是[0,1]是错误的; y=tan(ω(x-
y=tan(ω(x-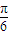 )+
)+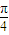 )=tan(ωx+
)=tan(ωx+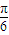 )?ω=
)?ω= -6k(k∈Z),
-6k(k∈Z),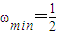 由此可判断④是错误的;
由此可判断④是错误的;

科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2013届浙江省瑞安十校高二第二学期期中理科数学试卷(解析版) 题型:填空题
对于函数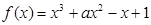 ,给出下列命题:
,给出下列命题:
①该函数必有2个极值; ②该函数的极大值必大于1;
③该函数的极小值必小于1;
④方程 =0一定有三个不等的实数根.
=0一定有三个不等的实数根.
其中正确的命题是 .(写出所有正确命题的序号)
查看答案和解析>>
科目:高中数学 来源:2013届福建省四地六校高二第一次联考理科数学 题型:填空题
对于函数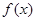 =x3+ax2-x+1,给出下列命题:
=x3+ax2-x+1,给出下列命题:
①该函数必有2个极值; ②该函数的极大值必大于1;
③该函数的极小值必小于1;
④方程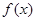 =0一定有三个不等的实数根.
=0一定有三个不等的实数根.
其中正确的命题是 .(写出所有正确命题的序号)
查看答案和解析>>
科目:高中数学 来源:福建省四地六校11-12学年高二下学期第一次联考试题数学理 题型:填空题
对于函数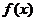 =x3+ax2-x+1,给出下列命题:
=x3+ax2-x+1,给出下列命题:
①该函数必有2个极值; ②该函数的极大值必大于1;
③该函数的极小值必小于1;
④方程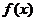 =0一定有三个不等的实数根.
=0一定有三个不等的实数根.
其中正确的命题是 .(写出所有正确命题的序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com