
(本小题满分12分)某电视台有一档综艺节目,其中有一个抢答环节,有甲、乙两位选手进行抢答,规则如下:若选手抢到答题权,答对得20分,答错或不答则送给对手10分。已知甲、乙两位选手抢到答题权的概率均相同,且每道题是否答对的机会是均等的, 若比赛进行两轮.
(1)求甲抢到1题的概率;
(2)求甲得到10分的概率.
(1)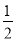 ;(2)
;(2) .
.
【解析】
试题分析:(1)本题属于古典概型概率问题,我们用列举法解题.甲乙两人进行两轮抢题,根据抢到的顺序所有可能是甲甲、甲乙、乙甲、乙乙四种情况,其中甲抢到一题的可能是2种,因此其概率应该是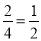 ;(2)各人得分情况,根据(1)中列举抢题情况,甲每题得分情况分别为甲甲:(0,0),(20,0),(0,20),(20,20),甲乙:(20,0),(20,10),(0,0),(0,10),乙甲:(0,20),(0,0),(10,20),(10,0),乙乙:(0,0),(10,0),(0,10),(10,10),各种得分情形有16种,其中得10的有4种,因此所求概率可求得为
;(2)各人得分情况,根据(1)中列举抢题情况,甲每题得分情况分别为甲甲:(0,0),(20,0),(0,20),(20,20),甲乙:(20,0),(20,10),(0,0),(0,10),乙甲:(0,20),(0,0),(10,20),(10,0),乙乙:(0,0),(10,0),(0,10),(10,10),各种得分情形有16种,其中得10的有4种,因此所求概率可求得为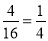 .
.
试题解析:(1)P=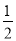 (2).甲得分的情况一共有16种情况,若两道题都是甲答,则甲得分情况为:(0,0),(20,0),(0,20),(20,20),若甲答第一题,乙答第二题,则甲得分情况为:(20,0),(20,10),(0,0),(0,10),若乙答第一题,甲答第二题,则甲得分情况为:(0,20),(0,0),(10,20),(10,0),若两题都是乙答,则甲得分情况为:(0,0),(0,10),(10,0),(10,10)。所以甲得10分的概率为:
(2).甲得分的情况一共有16种情况,若两道题都是甲答,则甲得分情况为:(0,0),(20,0),(0,20),(20,20),若甲答第一题,乙答第二题,则甲得分情况为:(20,0),(20,10),(0,0),(0,10),若乙答第一题,甲答第二题,则甲得分情况为:(0,20),(0,0),(10,20),(10,0),若两题都是乙答,则甲得分情况为:(0,0),(0,10),(10,0),(10,10)。所以甲得10分的概率为: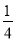
考点:古典概型.


科目:高中数学 来源:2014-2015学年湖北省黄冈市高三上学期元月调研考试理科数学试卷(解析版) 题型:解答题
设函数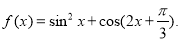
(Ⅰ)求函数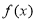 的最大值及此时
的最大值及此时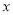 的取值集合;
的取值集合;
(Ⅱ)设 为
为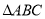 的三个内角,若
的三个内角,若 ,
,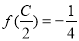 ,且
,且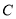 为锐角,求
为锐角,求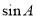 的值.
的值.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年江西省九江市第一次高考模拟统一考试理科数学试卷(解析版) 题型:解答题
(本小题满分10分)选修4—4:坐标系与参数方程
已知直线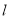 的参数方程为
的参数方程为 (
(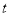 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,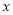 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线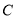 的极坐标方程是
的极坐标方程是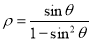 .
.
(1)写出直线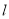 的极坐标方程与曲线
的极坐标方程与曲线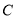 的普通方程;
的普通方程;
(2)若点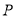 是曲线
是曲线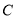 上的动点,求
上的动点,求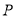 到直线
到直线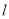 距离的最小值,并求出此时
距离的最小值,并求出此时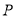 点的坐标.
点的坐标.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年江西省九江市第一次高考模拟统一考试理科数学试卷(解析版) 题型:选择题
在如下程序框图中,输入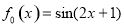 ,若输出的
,若输出的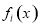 是
是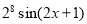 ,则程序框图中的判断框应填入( )
,则程序框图中的判断框应填入( )
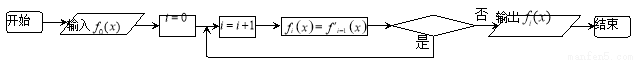
A.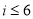 B.
B. C.
C.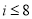 D.
D.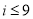
查看答案和解析>>
科目:高中数学 来源:2014-2015学年江西省景德镇高三第二质检文科数学试卷(解析版) 题型:解答题
(本小题满分10分)选修4-4:坐标系与参数方程
已知直线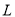 的参数方程为
的参数方程为 ,曲线
,曲线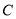 的参数方程为
的参数方程为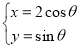 ,设直线
,设直线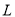 与曲线
与曲线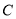 交于两点
交于两点
(1)求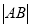 ;
;
(2)设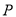 为曲线
为曲线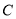 上的一点,当
上的一点,当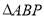 的面积取最大值时,求点
的面积取最大值时,求点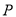 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年江西省景德镇高三第二质检文科数学试卷(解析版) 题型:选择题
执行以下程序框图,所得的结果为( )
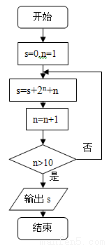
A.1067 B.2100 C.2101 D. 4160
查看答案和解析>>
科目:高中数学 来源:2014-2015学年湖南省长望浏宁四县高三3月调研(一模)考试理科数学试卷(解析版) 题型:填空题
已知两定点A(-1,0)和B(1,0),动点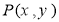 在直线
在直线 上移动,椭圆C
上移动,椭圆C
以A,B为焦点且经过点P,则椭圆C的离心率的最大值为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com