
已知两定点A(-1,0)和B(1,0),动点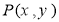 在直线
在直线 上移动,椭圆C
上移动,椭圆C
以A,B为焦点且经过点P,则椭圆C的离心率的最大值为 .
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:高中数学 来源:2014-2015学年江西省景德镇高三第二质检文科数学试卷(解析版) 题型:解答题
(本小题满分12分)某电视台有一档综艺节目,其中有一个抢答环节,有甲、乙两位选手进行抢答,规则如下:若选手抢到答题权,答对得20分,答错或不答则送给对手10分。已知甲、乙两位选手抢到答题权的概率均相同,且每道题是否答对的机会是均等的, 若比赛进行两轮.
(1)求甲抢到1题的概率;
(2)求甲得到10分的概率.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年湖南省长望浏宁四县高三3月调研(一模)考试文科数学试卷(解析版) 题型:选择题
将函数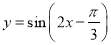 的图象向右平移
的图象向右平移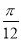 个单位,然后纵坐标不变横坐标伸长为原来的2倍,得到函数解析式为( ).
个单位,然后纵坐标不变横坐标伸长为原来的2倍,得到函数解析式为( ).
A.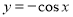 B.
B.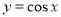 C.
C. D.
D.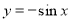
查看答案和解析>>
科目:高中数学 来源:2014-2015学年湖南省长望浏宁四县高三3月调研(一模)考试理科数学试卷(解析版) 题型:解答题
(本小题满分13分)为了加强环保建设,提高社会效益和经济效益,某市计划用若干年时间更换10000辆燃油型公交车。每更换一辆新车,则淘汰一辆旧车,更换的新车为电力型车和混合动力型车。今年初投入了电力型公交车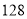 辆,混合动力型公交车
辆,混合动力型公交车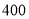 辆,计划以后电力型车每年的投入量比上一年增加
辆,计划以后电力型车每年的投入量比上一年增加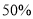 ,混合动力型车每年比上一年多投入
,混合动力型车每年比上一年多投入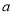 辆.设
辆.设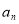 、
、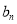 分别为第
分别为第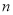 年投入的电力型公交车、混合动力型公交车的数量,设
年投入的电力型公交车、混合动力型公交车的数量,设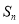 、
、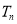 分别为
分别为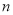 年里投入的电力型公交车、混合动力型公交车的总数量。
年里投入的电力型公交车、混合动力型公交车的总数量。
(1)求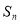 、
、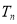 ,并求
,并求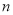 年里投入的所有新公交车的总数
年里投入的所有新公交车的总数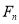 ;
;
(2)该市计划用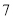 年的时间完成全部更换,求
年的时间完成全部更换,求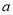 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年湖南省长望浏宁四县高三3月调研(一模)考试理科数学试卷(解析版) 题型:解答题
若数列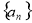 满足:存在正整数
满足:存在正整数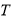 ,对于任意正整数
,对于任意正整数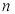 都有
都有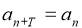 成立,则称数列
成立,则称数列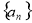 为周期数列,周期为
为周期数列,周期为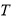 .已知数列
.已知数列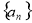 满足
满足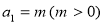 ,
, 则下列结论中错误的是( ).
则下列结论中错误的是( ).
A.若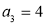 ,则
,则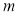 可以取3个不同的值;
可以取3个不同的值;
B.若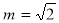 ,则数列
,则数列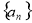 是周期为3的数列;
是周期为3的数列;
C.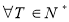 且
且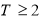 ,存在
,存在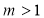 ,数列
,数列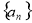 周期为
周期为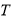 ;
;
D.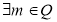 且
且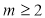 ,数列
,数列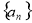 是周期数列.
是周期数列.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年湖南省长望浏宁四县高三3月调研(一模)考试理科数学试卷(解析版) 题型:选择题
已知函数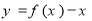 是偶函数,且
是偶函数,且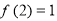 ,则
,则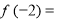 ( ).
( ).
A.-3 B.-1 C.1 D.2
查看答案和解析>>
科目:高中数学 来源:2014-2015学年湖北省毕业生二月调研考试文科数学试卷(解析版) 题型:选择题
从区间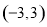 中任取两个整数
中任取两个整数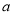 ,
,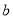 ,设点
,设点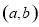 在圆
在圆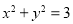 内的概率为
内的概率为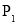 ,从区间
,从区间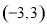 中任取两个实数
中任取两个实数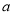 ,
,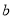 ,直线
,直线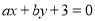 和圆
和圆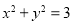 相离的概率为
相离的概率为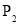 ,则( )
,则( )
A.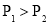 B.
B.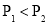
C.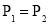 D.
D.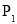 和
和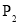 的大小关系无法确定
的大小关系无法确定
查看答案和解析>>
科目:高中数学 来源:2014-2015学年广东省潮州市高三上学期期末教学质量检测文科数学试卷(解析版) 题型:解答题
(本小题满分14分)已知椭圆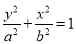 (
( )经过点
)经过点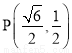 ,离心率为
,离心率为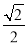 ,动点
,动点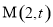 (
(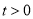 ).
).
(1)求椭圆的标准方程;
(2)求以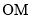 (
(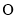 为坐标原点)为直径且被直线
为坐标原点)为直径且被直线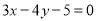 截得的弦长为
截得的弦长为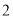 的圆的方程;
的圆的方程;
(3)设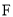 是椭圆的右焦点,过点
是椭圆的右焦点,过点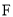 作
作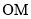 的垂线与以
的垂线与以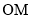 为直径的圆交于点
为直径的圆交于点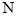 ,证明线段
,证明线段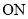 的长为定值,并求出这个定值.
的长为定值,并求出这个定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com