
【题目】(本题满分14分)
已知正项数列![]() 满足:对任意正整数
满足:对任意正整数![]() ,都有
,都有![]() 成等差数列,
成等差数列,![]() 成等比数列,且
成等比数列,且![]()
(Ⅰ)求证:数列![]() 是等差数列;
是等差数列;
(Ⅱ)求数列![]() 的通项公式;
的通项公式;
(Ⅲ) 设![]() 如果对任意正整数
如果对任意正整数![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)详见解析;(Ⅱ)详见解析;(Ⅲ)![]()
【解析】分析:(I)通过已知得到关于数列的项的两个等式,处理方程组得到![]() ,利用等差数列的定义得证;〔II〕利用等差数列的通项公式求出
,利用等差数列的定义得证;〔II〕利用等差数列的通项公式求出![]() ,求出
,求出![]() ;(III) 先通过裂项求和的方法求出
;(III) 先通过裂项求和的方法求出![]() ,代入
,代入![]() 化简得到关于
化简得到关于![]() 的二次不等式恒成立,构造新函数,通过对二次项系数的讨论求出函数的最大值,令最大值小于
的二次不等式恒成立,构造新函数,通过对二次项系数的讨论求出函数的最大值,令最大值小于![]() ,求出
,求出![]() 的范围.
的范围.
详解:(I)由已知,得![]() ①,
①,![]() ② .
② .
由②得![]() ③.将③代入①得,
③.将③代入①得,
对任意![]() ,有
,有![]()
即![]()
![]() 是等差数列.
是等差数列.
(Ⅱ)设数列![]() 的公差为
的公差为![]() ,
,
由![]() 经计算,得
经计算,得![]()
![]()
![]()
![]()
![]()
(Ⅲ)由(1)得![]()
![]()
不等式![]() 化为
化为![]()
即![]()
设![]()
![]() ,则
,则![]() 对任意正整数
对任意正整数![]() 恒成立.
恒成立.
当![]() ,即
,即![]() 时,不满足条件;
时,不满足条件;
当![]() ,即
,即![]() 时,满足条件;
时,满足条件;
当![]() ,即
,即![]() 时,
时,![]() 的对称轴为
的对称轴为![]() ,
,![]() 关于
关于![]() 递减,
递减,
因此,只需![]() 解得
解得![]()
综上,![]()


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】2002年国际数学家大会在北京召开,会标是以我国古代数学家赵爽的弦图为基础设计.弦图是由四个全等的直角三角形与一个小正方形拼成的一个大正方形(如图)如果小正方形的边长为1,大正方形的边长为5,直角三角形中较小的锐角为![]() ,则
,则![]() ( )
( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直角坐标系xoy中,其中A(0,0),B(2,0),C(1,1),D(0,1),图中圆弧所在圆的圆心为点C,半径为 ![]() ,且点P在图中阴影部分(包括边界)运动.若
,且点P在图中阴影部分(包括边界)运动.若 ![]() ,其中
,其中 ![]() ,则
,则 ![]() 的取值范围是( )
的取值范围是( )
A.[2,3+ ![]() ]
]
B.[2,3+ ![]() ]
]
C.[3- ![]() , 3+
, 3+ ![]() ]
]
D.[3- ![]() , 3+
, 3+ ![]() ]
]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足:a1=1,|an+1-an|=pn,n∈N*,Sn为数列{an}的前n项和.
(1)若{an}是递增数列,且a1,2a2,3a3成等差数列,求p的值;
(2)若p=![]() ,且{a2n-1}是递增数列,{a2n}是递减数列,求数列{an}的通项公式;
,且{a2n-1}是递增数列,{a2n}是递减数列,求数列{an}的通项公式;
(3)在(2)的条件下,令cn=n(an+1-an),求数列{cn}的前n项和Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知矩形ABCD中,E、F分别是AB、CD上的点,BE=CF=1,BC=2,AB=CD=3,P、Q分别为DE、CF的中点,现沿着EF翻折,使得二面角A﹣EF﹣B大小为 ![]() .
.
(Ⅰ)求证:PQ∥平面BCD;
(Ⅱ)求二面角A﹣DB﹣E的余弦值.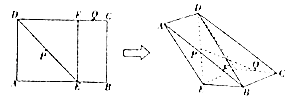
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过 ![]() 轴上动点
轴上动点 ![]() 引抛物线
引抛物线 ![]() 的两条切线
的两条切线 ![]() 、
、 ![]() ,
, ![]() 、
、 ![]() 为切点,设切线
为切点,设切线 ![]() 、
、 ![]() 的斜率分别为
的斜率分别为 ![]() 和
和 ![]() .
.
(Ⅰ)求证: ![]() ;
;
(Ⅱ)求证:直线 ![]() 恒过定点,并求出此定点坐标;
恒过定点,并求出此定点坐标;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC的面积为3,且满足0≤![]() ≤6,设
≤6,设![]() 与
与![]() 的夹角为θ.
的夹角为θ.
(1)求θ的取值范围;
(2)求函数f(θ)=2sin2![]() -
-![]() (cos θ+sin θ)·(cos θ-sin θ)的最大值与最小值.
(cos θ+sin θ)·(cos θ-sin θ)的最大值与最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在![]() 上的奇函数
上的奇函数![]() 满足
满足![]() ,且在
,且在![]() 上是增函数;
上是增函数;
定义行列式![]() ; 函数
; 函数![]() (其中
(其中![]() ).
).
(1) 证明: 函数![]() 在
在![]() 上也是增函数;
上也是增函数;
(2) 若函数![]() 的最大值为4,求
的最大值为4,求![]() 的值;
的值;
(3) 若记集合M={m|恒有g(![]() )<0},
)<0},![]() ,求
,求![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com