Question

【题目】如图，在直角坐标系xoy中，其中A(0,0),B(2,0),C(1,1),D(0,1),图中圆弧所在圆的圆心为点C，半径为 ，且点P在图中阴影部分（包括边界）运动.若 ，其中 ，则 的取值范围是（ ）

A.[2,3+ ]
B.[2,3+ ]
C.[3- , 3+ ]
D.[3- , 3+ ]

Answer 1

【答案】B
【解析】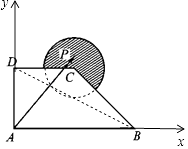

以A为坐标原点，AB为x轴，DA为y轴建立平面直角坐标系则
A（0，0），D（0，1），C（1，1），B（2，0）
直线BD的方程为x+2y﹣2=0，C到BD的距离d= ；
∴以点C为圆心，以 为半径的圆方程为（x﹣1）2+（y﹣1）2= ，
设P（m，n）则 =（m，n）， =（2，0）， =（﹣1，1）；
∴（m，n）=（2x﹣y，y）
∴m=2x﹣y，n=y，
∵P在圆内或圆上
∴（2x﹣y﹣1）2+（y﹣1）2≤ ，
设4x﹣y=t，则y=4x﹣t，代入上式整理得
80x2﹣（48t+16）x+8t2+7≤0，
设f（x）=80x2﹣（48t+16）x+8t2+7，x∈[ ， ]，
则 ，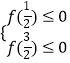
解得2≤t≤3+ ，
∴4x﹣y的取值范围是[2，3+ ]．
所以答案是：B
【考点精析】利用平面向量的坐标运算和圆的标准方程对题目进行判断即可得到答案，需要熟知坐标运算：设，则;;设，则；圆的标准方程：；圆心为A(a,b),半径为r的圆的方程．