
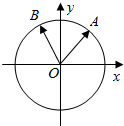
 如图,在平面直角坐标系中,锐角α和钝角β的终边分别与单位圆交于A,B两点,
如图,在平面直角坐标系中,锐角α和钝角β的终边分别与单位圆交于A,B两点,分析 (1)通过题意求出A、B点坐标,进而利用两角和的正弦公式计算即可;
(2)通过|AB|=$\frac{3}{2}$,利用$|\overrightarrow{OB}-\overrightarrow{OA}{|}^{2}$=$\frac{9}{4}$计算即得结论;
(3)通过设$\overrightarrow{OA}=(cosα,sinα)$,可知f(α)=3sinα-cosα,利用α为锐角即得结论.
解答 解:(1)由题意可得A的坐标为$(\frac{3}{5},\frac{4}{5})$,B点坐标$(-\frac{5}{13},\frac{12}{13})$,
根据三角函数定义,$sinα=\frac{3}{5},cosα=\frac{4}{5},sinβ=\frac{12}{13},cosβ=-\frac{5}{13}$,
∴$sin(α+β)=sinαcosβ+cosαsinβ=\frac{3}{5}×(-\frac{5}{13})+\frac{4}{5}×\frac{12}{13}=\frac{33}{65}$;
(2)∵|AB|=$\frac{3}{2}$,
∴$|\overrightarrow{AB}{|^2}=|\overrightarrow{OB}-\overrightarrow{OA}{|^2}={\overrightarrow{OB}^2}+{\overrightarrow{OA}^2}-2\overrightarrow{OA}•\overrightarrow{OB}=1+1-2cos<\overrightarrow{OA},\overrightarrow{OB}>=\frac{9}{4}$,
∴$cos<\overrightarrow{OA},\overrightarrow{OB}>=-\frac{1}{8}$,即$cos(β-α)=-\frac{1}{8}$;
(3)由题意可知,$\overrightarrow{OA}=(cosα,sinα)$,$\overrightarrow{OC}$=(-1,3 ),
∴f(α)=$\overrightarrow{OA}•\overrightarrow{OC}$=3sinα-cosα,
又∵α为锐角,
∴-1<f(α)<3.
点评 此题考查了两角和与差的正弦函数公式,熟练掌握公式是解本题的关键,注意解题方法的积累,属于中档题.


 智慧小复习系列答案
智慧小复习系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
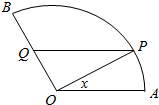 如图,准备在扇形空地AOB上修建一个山水景观OPQ,己知∠AOB=$\frac{2}{3}$π,OA=lkm,点P在扇形弧上,PQ∥OA交OB于点Q,记∠POA=x.
如图,准备在扇形空地AOB上修建一个山水景观OPQ,己知∠AOB=$\frac{2}{3}$π,OA=lkm,点P在扇形弧上,PQ∥OA交OB于点Q,记∠POA=x.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{2}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 16 | B. | -32 | C. | 256 | D. | -256 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com