
分析 (1)利用当生产10万件产品时,投入生产资金可达到39.8万元,求出a,可得投入资本y(万元)关于生产产品件数x(万件)的函数解析式;
(2)确定函数解析式,利用配方法求最值即可.
解答 解:(1)由题意:生产x万件产品的投入资本为y=20+a(x2-1)
∵当生产10万件产品时,投入资金为39.8万元,
∴39.8=20+a(102-1),
解得:a=0.2,
∴y=0.2x2+19.8;
(2)利润y=R(x)-(0.2x2+19.8)=160x-3.8x2-1480.2-0.2x2-19.8=-4x2+160x-1500=-4(x-20)2+100
当x=20时,y取最大值,
∴当生产20万件产品时利润最大,最大利润是100万元.
点评 本题考查函数模型的选择与应用,考查配方法,考查学生分析解决问题的能力,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:填空题
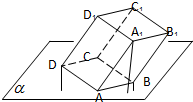 多面体上,位于同一条棱两端的顶点称为相邻的,如图,正方体的一个顶点A在平面α内,其余顶点在α的同侧,正方体上与顶点A相邻的三个顶点到α的距离分别为1,2和4,P是正方体的其余四个顶点中的一个,则P到平面α的距离可能是:(2)(4)(5)(6).(写出所有正确结论的编号)
多面体上,位于同一条棱两端的顶点称为相邻的,如图,正方体的一个顶点A在平面α内,其余顶点在α的同侧,正方体上与顶点A相邻的三个顶点到α的距离分别为1,2和4,P是正方体的其余四个顶点中的一个,则P到平面α的距离可能是:(2)(4)(5)(6).(写出所有正确结论的编号)查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若m?α,n?α,m∥n,则m∥α | B. | 若m⊥α,m?β,则α⊥β | ||
| C. | 若m?α,n?β,α∥β,则m∥n | D. | 若m⊥α,m⊥β,则α∥β |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{e}$ | B. | 1 | C. | e | D. | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 工作代码 | 工期/天 | 紧前工作 |
| A | 5 | 无 |
| B | 1 | A |
| C | 6 | A |
| D | 2 | A |
| E | 3 | B、C |
| F | 4 | B、C |
| 工作代码 | 工期/天 | 紧前工作 | 紧后工作 |
| A | 5 | 无 | |
| B | 1 | A | |
| C | 6 | A | |
| D | 2 | A | |
| E | 3 | B、C | |
| F | 4 | B、C |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com