
分析 以AB所在直线为x轴,AB的垂直平分线为y轴,建立坐标系,设∠COB=α(α∈(0,$\frac{π}{2}$)),利用$\overrightarrow{AC}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{AD}$,求出λ+μ=cosα+1,即可求出λ+μ的取值范围.
解答  解:以AB所在直线为x轴,AB的垂直平分线为y轴,建立坐标系,设∠COB=α(α∈(0,$\frac{π}{2}$)),则
解:以AB所在直线为x轴,AB的垂直平分线为y轴,建立坐标系,设∠COB=α(α∈(0,$\frac{π}{2}$)),则
A(-1,0),B(1,0),C(cosα,sinα),D(-cosα,sinα),
∵$\overrightarrow{AC}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{AD}$,
∴(cosα+1,sinα)=λ(2,0)+μ(-cosα+1,sinα),
∴2λ+μ(-cosα+1)=cosα+1,μ=1
∴λ=cosα,
∴λ+μ=cosα+1∈(1,2).
故答案为:(1,2).
点评 本题考查平面向量基本定理的运用,考查坐标法,考查学生分析解决问题的能力,正确建立坐标系是关键.


 星级口算天天练系列答案
星级口算天天练系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{16π}{3}+2\sqrt{3}$ | B. | $\frac{16π}{3}+4\sqrt{3}$ | C. | $\frac{24π}{3}+2\sqrt{3}$ | D. | $\frac{24π}{3}+4\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ① | B. | ② | C. | ③ | D. | ①③ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
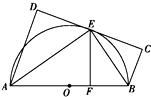 如图,AB为☉O的直径,直线CD与☉O相切于E,AD垂直CD于D,BC垂直CD于C,EF垂直AB于F,连接AE,BE.求证:∠FEB=∠CEB.
如图,AB为☉O的直径,直线CD与☉O相切于E,AD垂直CD于D,BC垂直CD于C,EF垂直AB于F,连接AE,BE.求证:∠FEB=∠CEB.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 价格x(元) | 9 | 9.5 | 10 | 10.5 | 11 |
| 销售量y(件) | 11 | a | 8 | 6 | 5 |
| A. | 7 | B. | 8.5 | C. | 9 | D. | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-$\frac{{e}^{2}+1}{2e}$) | B. | (-$\frac{{e}^{2}+1}{e}$,-2) | C. | (-2,0) | D. | ($\frac{{e}^{2}+1}{2e},+∞$) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com