解:(1)∵f(-1)=f(1),∴|1-a|=2+|a+1|①
又
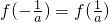
,
∴
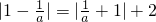
,即|1-a|=2|a|+|a+1|②
由①②得|a|=1,
∴a=±1.
又∵a=1时,①、②不成立,
故∴a=-1.
∴g(x)=-x
3+bx
2+cx,
设x
1、x
2是函数g(x)的两个极值点,则x
1、x
2是方程g′(x)=-3x
2+2bx+c=0的两个根,△=4b
2+12c>0(c为正整数),
∴x
1+x
2=
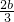
,
又∵A、O、B三点共线,
∴
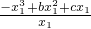
=
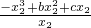
,
∴(x
1-x
2)[-(x
1+x
2)+b]=0,
又∵x
1≠x
2,
∴b=x
1+x
2=
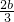
,
∴b=0.
(2)∵x≥0时,f(x)
min=2,
由g′(x)=-3x
2+c=0得
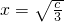
,可知g(x)在
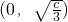
上单调递增,在
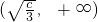
上单调递减,
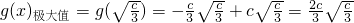
.
①由
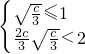
得c<3,∴c的值为1或2.(∵c为正整数)
②
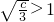
时,记g(x)在

上切线斜率为2的切点的横坐标为x
0,
则由g′(x)=-3x
2+c=2得
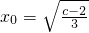
,依题意得g(x
0)<f(x
0),∴
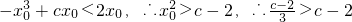
,得c<2,与c>3矛盾.
(或构造函数h(x)=2x-g(x)在x≥1上恒正)
综上,所求c的值为1或2.
分析:(1)根据f(-1)=f(1),且
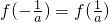
(a∈R,且a≠0),求出a的值,再对函数g(x)求导,根据函数g(x)=ax
3+bx
2+cx有两个不同的极值点,可以得到△>0,根据极值点共线A、B与坐标原点O可解出b的值.
(2)因为x≥0时,函数g(x)的图象恒在函数f(x)图象的下方,值当x≥0,g(x)恒小于f(x),所以g(x)的最大值恒小于f(x)的最小值,利用导数求出g(x)的最大值和f(x)的最小值,比较大小即可.
点评:本题考查了利用导数判断极值点的个数,以及比较函数大小问题.

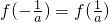 (a∈R,且a≠0),函数g(x)=ax3+bx2+cx(b∈R,c为正整数)有两个不同的极值点,且该函数图象上取得极值的两点A、B与坐标原点O在同一直线上.
(a∈R,且a≠0),函数g(x)=ax3+bx2+cx(b∈R,c为正整数)有两个不同的极值点,且该函数图象上取得极值的两点A、B与坐标原点O在同一直线上.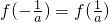 ,
,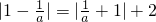 ,即|1-a|=2|a|+|a+1|②
,即|1-a|=2|a|+|a+1|②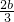 ,
,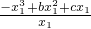 =
=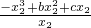 ,
,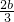 ,
,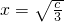 ,可知g(x)在
,可知g(x)在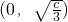 上单调递增,在
上单调递增,在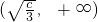
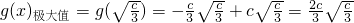 .
.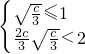 得c<3,∴c的值为1或2.(∵c为正整数)
得c<3,∴c的值为1或2.(∵c为正整数)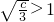 时,记g(x)在
时,记g(x)在 上切线斜率为2的切点的横坐标为x0,
上切线斜率为2的切点的横坐标为x0,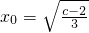 ,依题意得g(x0)<f(x0),∴
,依题意得g(x0)<f(x0),∴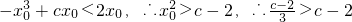 ,得c<2,与c>3矛盾.
,得c<2,与c>3矛盾.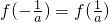 (a∈R,且a≠0),求出a的值,再对函数g(x)求导,根据函数g(x)=ax3+bx2+cx有两个不同的极值点,可以得到△>0,根据极值点共线A、B与坐标原点O可解出b的值.
(a∈R,且a≠0),求出a的值,再对函数g(x)求导,根据函数g(x)=ax3+bx2+cx有两个不同的极值点,可以得到△>0,根据极值点共线A、B与坐标原点O可解出b的值.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案