
已知向量a=3e1-2e2,b=4e1+e2,其中e1=(1,0),e2=(0,1),求:
(1)a·b,|a+b|;(2)a与b的夹角的余弦值.
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:高中数学 来源: 题型:
某工厂甲、乙、丙三个车间生产了同一种产品,数量分别为120件,80件,60件.为了解它们的产品质量是否存在显著差异,用分层抽样方法抽取了一个容量为n的样本进行调查,其中从丙车间的产品中抽取了3件,则n=( )
A.9 B.10
C.12 D.13
查看答案和解析>>
科目:高中数学 来源: 题型:
下列程序的功能是( )

A.求1×2×3×4×…×10 000的值
B.求2×4×6×8×…×10 000的值
C.求3×5×7×9×…×10 001的值
D.求满足1×3×5×…×n>10 000的最小正整数n
查看答案和解析>>
科目:高中数学 来源: 题型:
设数列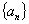 的前
的前 项和为
项和为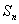 ,对任意的正整数
,对任意的正整数 ,都有
,都有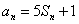 成立,记
成立,记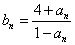 .(1)求数列
.(1)求数列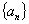 与数列
与数列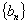 的通项公式;
的通项公式;
(2)设数列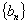 的前
的前 项和为
项和为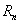 ,是否存在正整数
,是否存在正整数 ,使得
,使得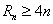 成立?若存在,找出一个正整数
成立?若存在,找出一个正整数 ;若不存在,请说明理由.
;若不存在,请说明理由.
(3)记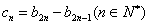 ,设数列
,设数列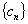 的前
的前 项和为
项和为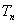 ,求证:对于
,求证:对于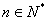 都有
都有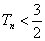
查看答案和解析>>
科目:高中数学 来源: 题型:
在平面直角坐标系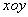 中,以原点
中,以原点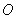 为圆心的圆
为圆心的圆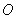 是曲线
是曲线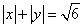 的内切圆.
的内切圆.
(1)求圆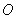 的方程;
的方程;
(2)若直线 与圆
与圆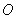 相切于第一象限,且与
相切于第一象限,且与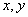 轴分别交于
轴分别交于 两点,当
两点,当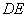 长最小时,求直线
长最小时,求直线 的方程;
的方程;
(3)设 是圆
是圆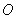 上任意两点,点
上任意两点,点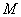 关于
关于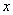 轴的对称点为
轴的对称点为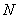 ,若直线
,若直线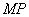 、
、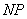 分别交于
分别交于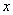 轴于点
轴于点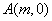 和
和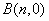 ,问这两点的横坐标之积
,问这两点的横坐标之积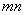 是否为定值?若是,请求出该定值;若不是,请说明理由.
是否为定值?若是,请求出该定值;若不是,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com