
分析 命题p:关于x的函数y=(a-1)x为增函数,则a-1>1,解得a范围;命题q:不等式-3x≤a对一切正实数均成立,可得a≥-1.若命题“p∨q”为真命题,且“p∧q”为假命题,则p与q一真一假.即可得出.
解答 解:命题p:关于x的函数y=(a-1)x为增函数,则a-1>1,解得a>2;
命题q:不等式-3x≤a对一切正实数均成立,∴a≥-1.
若命题“p∨q”为真命题,且“p∧q”为假命题,则p与q一真一假.
∴$\left\{\begin{array}{l}{a>2}\\{a<-1}\end{array}\right.$或$\left\{\begin{array}{l}{a≤2}\\{a≥-1}\end{array}\right.$,解得-1≤a≤2.
∴实数a的取值范围是[-1,2].
点评 本题考查了不等式的解法与性质、函数的单调性、简易逻辑的判定方法,考查了推理能力与计算能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
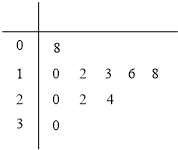 已知如图是某NBA球员连续10场常规赛得分的茎叶图,则该球员这10场比赛的场均得分为( )
已知如图是某NBA球员连续10场常规赛得分的茎叶图,则该球员这10场比赛的场均得分为( )| A. | 17.3 | B. | 17.5 | C. | 18.2 | D. | 18.4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,1] | B. | [-$\frac{{\sqrt{2}}}{2}$,$\frac{{\sqrt{2}}}{2}$] | C. | [-1,$\frac{{\sqrt{2}}}{2}$] | D. | [-$\frac{{\sqrt{2}}}{2}$,1] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,2] | B. | [2,+∞) | C. | (-∞,1] | D. | [1,+∞] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,4] | B. | [0,16] | C. | [-2,2] | D. | [1,4] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a≥4 | B. | a>4 | C. | a>3 | D. | a≤1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com