
分析 求导函数,利用f(x)的两个极值点分别是x1,x2,x1∈(-2,-1),x2∈(-1,0),建立不等式,利用平面区域,即可求2a+b的取值范围.
解答 解:由题意,f′(x)=x2+ax+2b.
∵f(x)的两个极值点分别是x1,x2,x1∈(-2,-1),x2∈(-1,0),
∴$\left\{\begin{array}{l}{f′(-2)=4-2a+2b>0}\\{f′(-1)=1-a+2b<0}\\{f′(0)=2b>0}\end{array}\right.$,
对应的平面区域如图所示: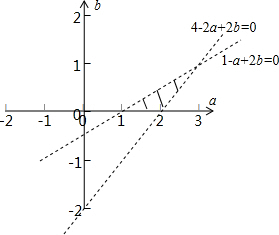
三个顶点坐标为(1,0),(2,0),(3,1),
则在(1,0)处,2a+b2,在(3,1)处,2a+b=7,
∴2a+b的取值范围是(2,7).
故答案为:(2,7).
点评 本题考查导数知识的运用,考查平面区域的运用,考查学生的计算能力,属于中档题.


 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 16 | B. | 8 | C. | 4 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | M∈a,a∈α | B. | M∈a,a?α | C. | M?a,a?α | D. | M?a,a∈α |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
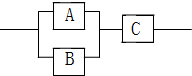 在一个由三个元件A,B,C构成的系统中,已知元件A,B,C正常工作的概率分别是$\frac{1}{2}$,$\frac{1}{3}$,$\frac{1}{4}$,且三个元件正常工作与否相互独立,则这个系统正常工作的概率为:$\frac{1}{6}$.
在一个由三个元件A,B,C构成的系统中,已知元件A,B,C正常工作的概率分别是$\frac{1}{2}$,$\frac{1}{3}$,$\frac{1}{4}$,且三个元件正常工作与否相互独立,则这个系统正常工作的概率为:$\frac{1}{6}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com