
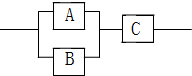
 在一个由三个元件A,B,C构成的系统中,已知元件A,B,C正常工作的概率分别是$\frac{1}{2}$,$\frac{1}{3}$,$\frac{1}{4}$,且三个元件正常工作与否相互独立,则这个系统正常工作的概率为:$\frac{1}{6}$.
在一个由三个元件A,B,C构成的系统中,已知元件A,B,C正常工作的概率分别是$\frac{1}{2}$,$\frac{1}{3}$,$\frac{1}{4}$,且三个元件正常工作与否相互独立,则这个系统正常工作的概率为:$\frac{1}{6}$. 分析 由题意用A,B,C三个不同的元件连接成一个系统N.当元件C正常工作且元件A,B至少有一个正常工作时,系统正常工作.先算出A,B至少有一个通的概率,再利用乘法原理求值.
解答 解:A,B都不工作的概率为(1-$\frac{1}{2}$)(1-$\frac{1}{3}$)=$\frac{1}{3}$,
故A,B至少有一个正常工作的概率是$\frac{2}{3}$.
又元件C正常工作的概率依次为$\frac{1}{4}$,
故系统能正常工作的概率等于$\frac{2}{3}$×$\frac{1}{4}$=$\frac{1}{6}$.
故答案为$\frac{1}{6}$.
点评 本题考查相互独立事件的概率乘法公式,解题的关键是求出A,B所组成的系统能正确常工作的概率,理解并掌握乘法原理是解答本题的知识保证.


 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{bn-am}{n-m}$ | B. | $\frac{bm-an}{n-m}$ | C. | $\frac{bn+am}{n+m}$ | D. | $\frac{bm+an}{n+m}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 22017 | B. | -22017 | C. | 21008 | D. | -21008 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|-3<x<-$\frac{3}{2}$} | B. | {x|x>1} | C. | {x|x>3} | D. | {x|$\frac{3}{2}$<x<3} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com