
| A. | a≤0 | B. | a<0 | C. | a≥0 | D. | a>0 |
分析 根据导数法确定函数单调性的方法和步骤,我们易求出函数f(x)=x3-ax在R上增函数时a的取值范围,然后根据“谁小谁充分,谁大认谁必要”的原则,结合题目中的四个答案,即可得到结论.
解答 解:∵函数f(x)=x3-ax的导函数为:
f'(x)=3x2-a,
当a<0时,f'(x)>0恒成立,
则函数f(x)=x3-ax在R上增函数,
但函数f(x)=x3-ax在R上增函数时,
f'(x)≥0恒成立,故a≤0,
故A是充要条件,B是充分不必要条件,
C、D是既不充分也不必要条件,
故选:B.
点评 本题考查的知识点是利用导数研究函数的单调性,充要条件的判定,其中根据“谁小谁充分,谁大认谁必要”的原则,求a的取舍范围,是解答本题的关键.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{16}{29}$ | B. | $\frac{15}{28}$ | C. | $\frac{5}{9}$ | D. | $\frac{8}{15}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{3}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{6}$ | D. | $\frac{π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
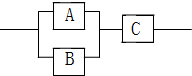 在一个由三个元件A,B,C构成的系统中,已知元件A,B,C正常工作的概率分别是$\frac{1}{2}$,$\frac{1}{3}$,$\frac{1}{4}$,且三个元件正常工作与否相互独立,则这个系统正常工作的概率为:$\frac{1}{6}$.
在一个由三个元件A,B,C构成的系统中,已知元件A,B,C正常工作的概率分别是$\frac{1}{2}$,$\frac{1}{3}$,$\frac{1}{4}$,且三个元件正常工作与否相互独立,则这个系统正常工作的概率为:$\frac{1}{6}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com