
【题目】在海岸A处,发现北偏东45°方向,距A处( ![]() ﹣1)海里的B处有一艘走私船,在A处北偏西75°方向,距A处2海里的C处的缉私船奉命以10
﹣1)海里的B处有一艘走私船,在A处北偏西75°方向,距A处2海里的C处的缉私船奉命以10 ![]() 海里/小时的速度追截走私船,此时走私船正以10海里/小时的速度从B处向北偏东30°的方向逃窜,问缉私船沿什么方向能最快追上走私船,并求出所需要的时间.
海里/小时的速度追截走私船,此时走私船正以10海里/小时的速度从B处向北偏东30°的方向逃窜,问缉私船沿什么方向能最快追上走私船,并求出所需要的时间. 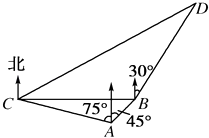
【答案】解:如图所示,设缉私船追上走私船需t小时, 则有CD= ![]() ,BD=10t.在△ABC中,
,BD=10t.在△ABC中,
∵AB= ![]() ﹣1,AC=2,
﹣1,AC=2,
∠BAC=45°+75°=120°.
根据余弦定理可求得BC= ![]() .
.
∠CBD=90°+30°=120°.
在△BCD中,根据正弦定理可得
sin∠BCD= ![]() ,
,
∵∠CBD=120°,∴∠BCD=30°,∠BDC=30°,
∴BD=BC= ![]() ,则有
,则有
10t= ![]() ,t=
,t= ![]() =0.245(小时)=14.7(分钟).
=0.245(小时)=14.7(分钟).
所以缉私船沿北偏东60°方向,需14.7分钟才能追上走私船.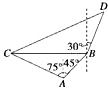
【解析】设缉私船追上走私船需t小时,进而可表示出CD和BD,进而在△ABC中利用余弦定理求得BC,进而在△BCD中,根据正弦定理可求得sin∠BCD的值,进而求得∠BDC=∠BCD=30°进而求得BD,进而利用BD=10t求得t.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]()
(1)求函数![]() 的极值;
的极值;
(2)若![]() 时,函数
时,函数![]() 有且只有一个零点,求实数
有且只有一个零点,求实数![]() 的值;
的值;
(3若![]() ,对于区间
,对于区间![]() 上的任意两个不相等的实数
上的任意两个不相等的实数![]() ,都有
,都有![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点A(﹣ ![]() ,0),B(
,0),B( ![]() ,0),P是平面内的一个动点,直线PA与PB交于点P,且它们的斜率之积是﹣
,0),P是平面内的一个动点,直线PA与PB交于点P,且它们的斜率之积是﹣ ![]() .
.
(1)求动点P的轨迹C的方程;
(2)设直线l:y=kx+1与曲线C交于M、N两点,当线段MN的中点在直线x+2y=0上时,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,|φ|< ![]() )的部分图象如图所示.
)的部分图象如图所示. 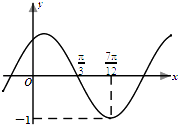
(1)求函数y=f(x)的解析式;
(2)求函数y=f(x)的单调增区间;
(3)求方程f(x)=0的解集.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】渝州集团对所有员工进行了职业技能测试从甲、乙两部门中各任选10名员工的测试成绩(单位:分)数据的茎叶图如图所示.
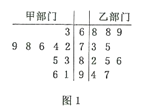
(1)若公司决定测试成绩高于85分的员工获得“职业技能好能手”称号,求从这20名员工中任选三人,其中恰有两人获得“职业技能好能手”的概率;
(2)公司结合这次测试成绩对员工的绩效奖金进行调整(绩效奖金方案如下表),若以甲部门这10人的样本数据来估计该部门总体数据,且以频率估计概率,从甲部门所有员工中任选3名员工,记绩效奖金不小于![]() 的人数为
的人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com