
【题目】已知函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,|φ|< ![]() )的部分图象如图所示.
)的部分图象如图所示. 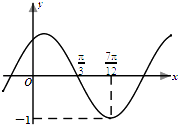
(1)求函数y=f(x)的解析式;
(2)求函数y=f(x)的单调增区间;
(3)求方程f(x)=0的解集.
【答案】
(1)解:由图知,A=1,
∵周期T=4( ![]() ﹣
﹣ ![]() )=π,
)=π,
∴ω= ![]() =2,
=2,
∴f(x)=sin(2x+φ),
又f( ![]() )=﹣1,
)=﹣1,
∴sin( ![]() +φ)=﹣1,
+φ)=﹣1,
∴ ![]() +φ=2kπ+
+φ=2kπ+ ![]() (k∈Z),
(k∈Z),
∴φ=2kπ+ ![]() (k∈Z),又|φ|<
(k∈Z),又|φ|< ![]() ,
,
∴φ= ![]() ,
,
∴f(x)=sin(2x+ ![]() )
)
(2)解:﹣ ![]() +2kπ≤2x+
+2kπ≤2x+ ![]() ≤
≤ ![]() +2kπ,k∈Z.
+2kπ,k∈Z.
∴﹣ ![]() +kπ≤x≤
+kπ≤x≤ ![]() +kπ,k∈Z.
+kπ,k∈Z.
∴函数y=f(x)的单调增区间为:[﹣ ![]() +kπ,
+kπ, ![]() +kπ]k∈Z
+kπ]k∈Z
(3)解:∵f(x)=0,
∴2x+ ![]() =kπ,k∈Z.
=kπ,k∈Z.
∴x=﹣ ![]() +
+ ![]() kπ,k∈Z.
kπ,k∈Z.
∴方程f(x)=0的解集为{x|x=﹣ ![]() +
+ ![]() kπ,k∈Z}
kπ,k∈Z}
【解析】(1)由图知,A=1,T=π,于是知ω=2;再由f( ![]() )=﹣1,可求得φ=2kπ+
)=﹣1,可求得φ=2kπ+ ![]() (k∈Z),又|φ|<
(k∈Z),又|φ|< ![]() ,于是可得φ及函数y=f(x)的解析式;(2)利用正弦函数的单调性,由﹣
,于是可得φ及函数y=f(x)的解析式;(2)利用正弦函数的单调性,由﹣ ![]() +2kπ≤2x+
+2kπ≤2x+ ![]() ≤
≤ ![]() +2kπ(k∈Z)可求函数y=f(x)的单调增区间;(3)f(x)=02x+
+2kπ(k∈Z)可求函数y=f(x)的单调增区间;(3)f(x)=02x+ ![]() =kπ(k∈Z),从而可求得方程f(x)=0的解集.
=kπ(k∈Z),从而可求得方程f(x)=0的解集.
【考点精析】本题主要考查了函数y=Asin(ωx+φ)的图象变换的相关知识点,需要掌握图象上所有点向左(右)平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的横坐标伸长(缩短)到原来的
的图象上所有点的横坐标伸长(缩短)到原来的![]() 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的纵坐标伸长(缩短)到原来的
的图象上所有点的纵坐标伸长(缩短)到原来的![]() 倍(横坐标不变),得到函数
倍(横坐标不变),得到函数![]() 的图象才能正确解答此题.
的图象才能正确解答此题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】设等差数列{an}的前项和为Sn , 且a2=2,S5=15,数列{bn}的前项和为Tn , 且b1= ![]() ,2nbn+1=(n+1)bn(n∈N*)
,2nbn+1=(n+1)bn(n∈N*)
(Ⅰ)求数列{an}通项公式an及前项和Sn;
(Ⅱ) 求数列{bn}通项公式bn及前项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】己知命题p:方程 ![]() 表示焦点在y轴的椭圆;命题q:关于x的不等式x2﹣2x+m>0的解集是R; 若“p∧q”是假命题,“p∨q”是真命题,求实数m的取值范围.
表示焦点在y轴的椭圆;命题q:关于x的不等式x2﹣2x+m>0的解集是R; 若“p∧q”是假命题,“p∨q”是真命题,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A、B、C为△ABC的三个内角,且其对边分别为a、b、c,若cosBcosC﹣sinBsinC= ![]() .
.
(1)求角A;
(2)若a=2 ![]() ,b+c=4,求△ABC的面积.
,b+c=4,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在海岸A处,发现北偏东45°方向,距A处( ![]() ﹣1)海里的B处有一艘走私船,在A处北偏西75°方向,距A处2海里的C处的缉私船奉命以10
﹣1)海里的B处有一艘走私船,在A处北偏西75°方向,距A处2海里的C处的缉私船奉命以10 ![]() 海里/小时的速度追截走私船,此时走私船正以10海里/小时的速度从B处向北偏东30°的方向逃窜,问缉私船沿什么方向能最快追上走私船,并求出所需要的时间.
海里/小时的速度追截走私船,此时走私船正以10海里/小时的速度从B处向北偏东30°的方向逃窜,问缉私船沿什么方向能最快追上走私船,并求出所需要的时间. 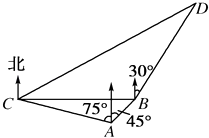
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知:空间四边形ABCD如图所示,E、F分别是AB、AD的中点,G、H分别是BC,CD上的点,且 ![]() .
. ![]() ,则直线FH与直线EG( )
,则直线FH与直线EG( ) 
A.平行
B.相交
C.异面
D.垂直
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校100名学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.

(Ⅰ)求图中![]() 的值;
的值;
(Ⅱ)根据频率分布直方图,估计这100名学生语文成绩的平均分;
(Ⅲ)若这100名学生语文成绩某些分数段的人数(![]() )与数学成绩相应分数段的人数(
)与数学成绩相应分数段的人数(![]() )之比如表所示,求数学成绩在
)之比如表所示,求数学成绩在![]() 之外的人数.
之外的人数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C的方程为:x2+y2﹣2mx﹣2y+4m﹣4=0,(m∈R).
(1)试求m的值,使圆C的面积最小;
(2)求与满足(1)中条件的圆C相切,且过点(1,﹣2)的直线方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 的参数方程为
的参数方程为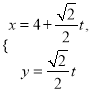 (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点, ![]() 轴的非负半轴为极轴建立极坐标系,圆
轴的非负半轴为极轴建立极坐标系,圆![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 与圆
与圆![]() 交于
交于![]() ,
, ![]() 两点.
两点.
(1)求圆![]() 的直角坐标方程及弦
的直角坐标方程及弦![]() 的长;
的长;
(2)动点![]() 在圆
在圆![]() 上(不与
上(不与![]() ,
, ![]() 重合),试求
重合),试求![]() 的面积的最大值.
的面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com