
(12分)(原创)已知函数 满足以下条件:①定义在正实数集上;②
满足以下条件:①定义在正实数集上;②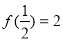 ;③对任意实数
;③对任意实数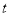 ,都有
,都有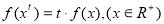 。
。
(1)求 ,
,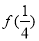 的值;
的值;
(2)求证:对于任意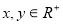 ,都有
,都有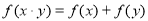 ;
;
(3)若不等式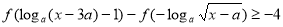 ,对
,对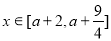 恒成立,求实数
恒成立,求实数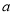 的取值范围。
的取值范围。
【解析】
试题分析:先利用赋值法求出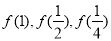 ,(2)根据抽象函数表达式可以看出只是一个对数函数模型,借助
,(2)根据抽象函数表达式可以看出只是一个对数函数模型,借助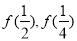 可以求出函数原型:
可以求出函数原型: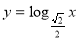 ,但证明时需利用
,但证明时需利用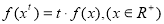 ,所以取两个指数型的正数,
,所以取两个指数型的正数,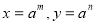 去考察
去考察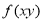 和
和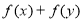 即可;(3)首先利用赋值法证明函数在
即可;(3)首先利用赋值法证明函数在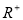 上是减函数,再考虑式子在
上是减函数,再考虑式子在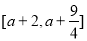 上有意义,求出
上有意义,求出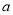 的要求,即定义域优先考虑,然后要求
的要求,即定义域优先考虑,然后要求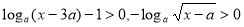 ,最后借助函数是减函数,解不等式
,最后借助函数是减函数,解不等式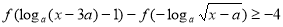 ,即
,即
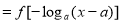 ,最终求出
,最终求出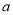 的范围,本题难度较大,需认真解每一步.
的范围,本题难度较大,需认真解每一步.
试题解析:(1)令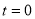 ,得:
,得: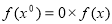 ,
,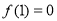 ,
,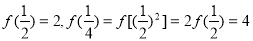 ,
,
(2)证明:设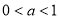 ,
,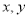 均为正数 ,则存在
均为正数 ,则存在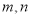 使得
使得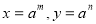 ,
,
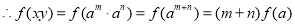
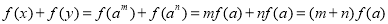
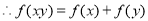
(3)先证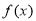 在正实数集上单调递减:
在正实数集上单调递减:
设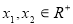 ,且
,且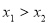 ,令:
,令: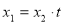 ,(
,(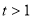 ),
),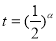 ,
,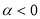 , 则由(2)知
, 则由(2)知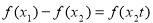
-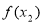 =
=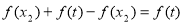 =
=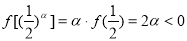
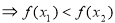 ,则函数
,则函数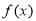 在
在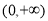 上是减函数.
上是减函数.
再求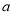 取值范围:
取值范围:
因为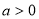 且
且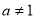 ,又
,又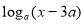 ,
,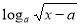 在区间
在区间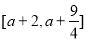 上有定义
上有定义
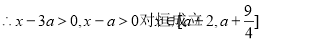

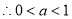
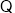 定义在正实数集上
定义在正实数集上  可得:
可得:
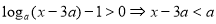 ,对
,对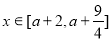 恒成立,
恒成立,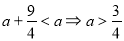 ……(1)
……(1)
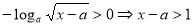 ,对
,对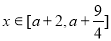 恒成立,
恒成立,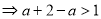 恒成立……(2)
恒成立……(2)
由(2)中令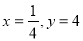 ,得:
,得: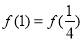
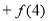
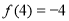 ,则原不等式可整理为:
,则原不等式可整理为:

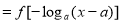
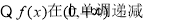
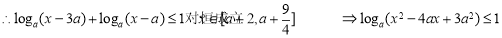
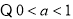 直线
直线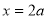 在
在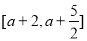 左侧,令
左侧,令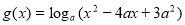
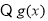 在
在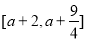 上为减函数,需要
上为减函数,需要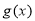 最大值为
最大值为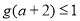 ,即
,即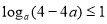 ,
,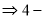
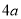
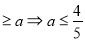 (3),有上面(1)(2)(3)得:
(3),有上面(1)(2)(3)得: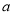 的取值范围是
的取值范围是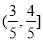
考点:1.赋值法;2.抽象函数的单调性的证明;3.利用抽象函数的增减性解不等式;


 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案科目:高中数学 来源:2014-2015学年甘肃省高二上学期期末考试数学试卷(解析版) 题型:选择题
设双曲线 的一条渐近线与抛物线
的一条渐近线与抛物线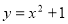 只有一个公共点,则双曲线的离心率为( )
只有一个公共点,则双曲线的离心率为( )
A.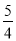 B.
B.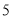 C.
C.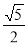 D.
D.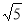
查看答案和解析>>
科目:高中数学 来源:2014-2015学年上海市闸北区高三上学期期末练习文科数学试卷(解析版) 题型:解答题
请仔细阅读以下材料:
已知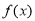 是定义在
是定义在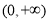 上的单调递增函数.
上的单调递增函数.
求证:命题“设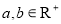 ,若
,若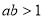 ,则
,则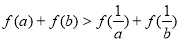 ”是真命题.
”是真命题.
证明:因为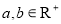 ,由
,由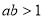 得
得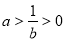 .
.
又因为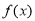 是定义在
是定义在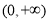 上的单调递增函数,
上的单调递增函数,
于是有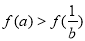 . ①
. ①
同理有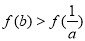 . ②
. ②
由① + ②得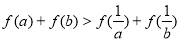 .
.
故,命题“设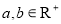 ,若
,若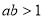 ,则
,则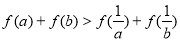 ”是真命题.
”是真命题.
请针对以上阅读材料中的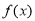 ,解答以下问题:
,解答以下问题:
(1)试用命题的等价性证明:“设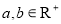 ,若
,若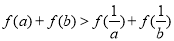 ,则:
,则: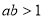 ”是真命题;
”是真命题;
(2)解关于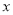 的不等式
的不等式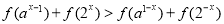 (其中
(其中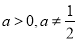 ).
).
查看答案和解析>>
科目:高中数学 来源:2014-2015学年上海市闸北区高三上学期期末练习理科数学试卷(解析版) 题型:解答题
对于集合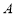 ,定义了一种运算“
,定义了一种运算“ ”,使得集合
”,使得集合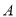 中的元素间满足条件:如果存在元素
中的元素间满足条件:如果存在元素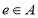 ,使得对任意
,使得对任意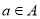 ,都有
,都有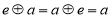 ,则称元素
,则称元素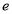 是集合
是集合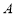 对运算“
对运算“ ”的单位元素.例如:
”的单位元素.例如: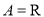 ,运算“
,运算“ ”为普通乘法;存在
”为普通乘法;存在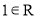 ,使得对任意
,使得对任意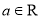 ,都有
,都有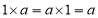 ,所以元素
,所以元素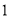 是集合
是集合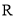 对普通乘法的单位元素.
对普通乘法的单位元素.
下面给出三个集合及相应的运算“ ”:
”:
①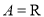 ,运算“
,运算“ ”为普通减法;
”为普通减法;
②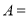 {
{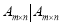 表示
表示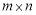 阶矩阵,
阶矩阵,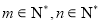 },运算“
},运算“ ”为矩阵加法;
”为矩阵加法;
③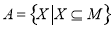 (其中
(其中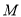 是任意非空集合),运算“
是任意非空集合),运算“ ”为求两个集合的交集.
”为求两个集合的交集.
其中对运算“ ”有单位元素的集合序号为
”有单位元素的集合序号为
A.①② B.①③ C.①②③ D.②③
查看答案和解析>>
科目:高中数学 来源:2014-2015学年重庆市高一上学期第三次定时练习数学试卷(解析版) 题型:解答题
(本题满分13分)(1)已知角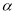 的顶点在原点,始边与
的顶点在原点,始边与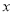 轴的非负半轴重合,终边经过点
轴的非负半轴重合,终边经过点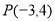 ,
,
求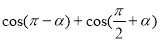 的值。
的值。
(2)若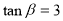 ,求
,求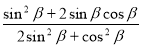 的值。
的值。
查看答案和解析>>
科目:高中数学 来源:2014-2015学年重庆市高一上学期第三次定时练习数学试卷(解析版) 题型:选择题
已知[x]表示不超过实数x的最大整数, 为取整函数,
为取整函数, 是方程
是方程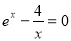 的根 (e为自然对数的底数),则
的根 (e为自然对数的底数),则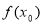 等于 ( )
等于 ( )
A.4 B.3 C.2 D.1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com