
已知函数 ,那么下列命题中假命题是( )
,那么下列命题中假命题是( )
A. 既不是奇函数,也不是偶函数 既不是奇函数,也不是偶函数 | B. 在 在 上恰有一个零点 上恰有一个零点 |
C. 是周期函数 是周期函数 | D. 在 在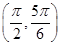 上是增函数 上是增函数 |
B
解析试题分析:∵f(x)=cos2x+sinx,∴f(-x)=cos2x-sinx,故f(x)既不是奇函数也不是偶函数,即A是真命题;∵由f(x)=cos2x+sinx=1-sin2x+sinx=0,得sinx= ,∴f(x)在[-π,0]上恰有2个零点,即B是假命题;∵f(x)=cos2x+sinx=1-sin2x+sinx=-(sinx-
,∴f(x)在[-π,0]上恰有2个零点,即B是假命题;∵f(x)=cos2x+sinx=1-sin2x+sinx=-(sinx-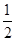 )2+
)2+ ,∴f(x)是周期函数,即C是真命题;∵f(x)=cos2x+sinx=1-sin2x+sinx=-(sinx-
,∴f(x)是周期函数,即C是真命题;∵f(x)=cos2x+sinx=1-sin2x+sinx=-(sinx-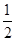 )2+
)2+ ,∴f(x)在
,∴f(x)在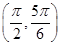 上是增函数,即D是真命题.故选B.
上是增函数,即D是真命题.故选B.
考点:本题考查了三角函数的性质及命题的真假判断
点评:解此类试题时要注意三角函数恒等变换及性质的灵活运用,属基础题


 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案科目:高中数学 来源: 题型:单选题
将函数 的图象向左平移
的图象向左平移 后得到函数
后得到函数 ,则
,则 具有性质( )
具有性质( )
A.最大值为 ,图象关于直线 ,图象关于直线 对称 对称 | B.周期为 ,图象关于 ,图象关于 对称 对称 |
C.在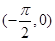 上单调递增,为偶函数 上单调递增,为偶函数 | D.在 上单调递增,不为奇函数 上单调递增,不为奇函数 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com