
分析 (1)利用等差数列的通项公式及其求和公式即可得出.
(2)假设1,$\sqrt{3}$,2分别为等差数列{an}中第m,n,r项,则$\left\{\begin{array}{l}{1={a}_{1}+(m-1)d}\\{\sqrt{3}={a}_{1}+(n-1)d}\\{2={a}_{1}+(r-1)d}\end{array}\right.$,可得$\sqrt{3}$-1=$\frac{n-m}{r-m}$,而左边为无理数,右边为有理数即可得出矛盾.
解答 (1)解:∵数列{$\frac{{S}_{n}}{{a}_{n}}$}是等差数列,
∴$2×\frac{{S}_{2}}{{a}_{2}}$=$\frac{{S}_{1}}{{a}_{1}}$+$\frac{{S}_{3}}{{a}_{3}}$,∴$\frac{2(2+d)}{1+d}$=1+$\frac{3+3d}{1+2d}$,化为d2-d=0,∵d≠0,解得d=1.
∴an=1+(n-1)=n.
(2)证明:假设1,$\sqrt{3}$,2分别为等差数列{an}中第m,n,r项,
则$\left\{\begin{array}{l}{1={a}_{1}+(m-1)d}\\{\sqrt{3}={a}_{1}+(n-1)d}\\{2={a}_{1}+(r-1)d}\end{array}\right.$,
解得$\sqrt{3}$-1=$\frac{n-m}{r-m}$,
∵m,n,r为正整数,∴上式左端为无理数,右端为有理数,故等式不能成立,
因此,假设不成立,因此1,$\sqrt{3}$,2不可能为等差数列{an}中的三项.
点评 本题考查了等差数列的通项公式及其求和公式、实数的性质、反证法,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,1,1) | B. | ($\frac{1}{3}$,$\frac{1}{3}$,$\frac{1}{3}$) | ||
| C. | ($\frac{\sqrt{3}}{3}$,$\frac{\sqrt{3}}{3}$,$\frac{\sqrt{3}}{3}$) | D. | ($\frac{\sqrt{3}}{3}$,$\frac{\sqrt{3}}{3}$,$\frac{\sqrt{3}}{3}$)或(-$\frac{\sqrt{3}}{3}$,-$\frac{\sqrt{3}}{3}$,-$\frac{\sqrt{3}}{3}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{39}}}{39}$ | B. | $\frac{{\sqrt{13}}}{13}$ | C. | $\frac{{\sqrt{13}}}{39}$ | D. | $\frac{{\sqrt{39}}}{13}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
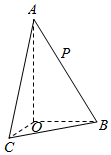 如图所示,AO⊥平面BOC,∠OAB=30°,△AOC与△AOB全等,且二面角B-AO-C是直二面角,动点P在线段AB上,则CP与平面AOB所成角的正切的最大值为( )
如图所示,AO⊥平面BOC,∠OAB=30°,△AOC与△AOB全等,且二面角B-AO-C是直二面角,动点P在线段AB上,则CP与平面AOB所成角的正切的最大值为( )| A. | 1 | B. | $\sqrt{3}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{2\sqrt{3}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
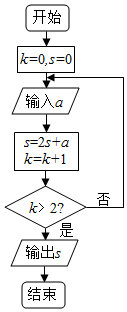 秦九韶是我国南宋时期的数学家,他在所著的《数学九章》中提出多项式求值的秦九韶算法,如图所示的程序框图给出了利用秦九韶算法求多项式值的一个实例,依次输入a为2,2,5,则输出的s=( )
秦九韶是我国南宋时期的数学家,他在所著的《数学九章》中提出多项式求值的秦九韶算法,如图所示的程序框图给出了利用秦九韶算法求多项式值的一个实例,依次输入a为2,2,5,则输出的s=( )| A. | 7 | B. | 12 | C. | 17 | D. | 34 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com