Question

13．如图，在四面体ABCD中，平面ADC⊥平面ABC，△ADC是以AC为斜边的等腰直角三角形，已知EB⊥平面ABC，AC=2EB．
（Ⅰ）求证：DE∥平面ABC；
（Ⅱ）若AC⊥BC，AC=1，BC=2，求四面体DBCE的体积．

Answer 1

分析 （Ⅰ）设F是AC中点，连结DF，BF．只需，$DF=\frac{1}{2}AC=EB$，即四边形DEBF是平行四边形，DE∥FB，可证得DE∥平面ABC．
（Ⅱ）证得DF∥平面CBE，可得D到平面CBE距离等于F到平面CBE距离，故V_D-BCE=V_F-BCE，四面体BCDE的体积是${V_{BCDE}}=\frac{1}{3}{S_{△BCF}}×FC=\frac{1}{3}•\frac{1}{2}•\frac{1}{2}=\frac{1}{12}$．

解答 解：（Ⅰ）设F是AC中点，连结DF，BF．
因为△ADC是以AC为斜边的等腰直角三角形，所以DF⊥AC．
因为平面ADC⊥平面ABC，交线是AC，所以DF⊥平面ABC．…（2分）
因为EB⊥平面ABC，所以DF∥EB．…（4分）
因为，$DF=\frac{1}{2}AC=EB$，所以四边形DEBF是平行四边形，所以DE∥FB．
因为DE?平面ABC，FB?平面ABC，所以DE∥平面ABC．…（6分）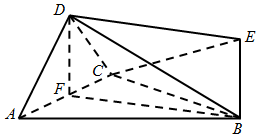

（Ⅱ）因为AC⊥BC，AC⊥EB，所以AC⊥平面CBE，
故F到平面CBE距离$FC=\frac{1}{2}$．…（8分）
因为DF∥EB，所以DF∥平面CBE，故D到平面CBE距离等于F到平面CBE距离，故V_D-BCE=V_F-BCE．…（10分）
因为$EB=\frac{1}{2}$，所以${S_{△BCF}}=\frac{1}{2}×EB×BC=\frac{1}{2}$，
因此四面体BCDE的体积是${V_{BCDE}}=\frac{1}{3}{S_{△BCF}}×FC=\frac{1}{3}•\frac{1}{2}•\frac{1}{2}=\frac{1}{12}$．…（12分）

点评 本题考查了线面平行的判定，几何体的体积计算，属于中档题．