
分析 (1)把y轴向左平移2个单位变为x=-2,此时点M到直线x=-2的距离等于它到点(2,0)的距离,即可得到点M的轨迹方程.
(2)设直线l的倾斜解为α,则l与y轴的夹角θ=90°-α,cotθ=tanα=2,sinθ=$\frac{1}{\sqrt{5}}$,然后求出|AB|.
解答 解:(1)因为动点M(x,y)到点F(2,0)的距离比它到y轴的距离大2,
所以点M到直线x=-2的距离等于它到点(2,0)的距离,
因此点M的轨迹为抛物线,方程为y2=8x.
(2)设直线l的倾斜角为α,则l与y轴的夹角θ=90°-α,
由题意,cotθ=tanα=2,
∴sinθ=$\frac{1}{\sqrt{5}}$,
∴|AB|=$\frac{8}{si{n}^{2}θ}$=40.
点评 本题考查点M的轨迹方程,考查抛物线的定义,考查抛物线的焦点弦的求法,正确运用抛物线的定义是关键.


科目:高中数学 来源: 题型:选择题
| A. | R | B. | ∅ | C. | (0,2] | D. | (-∞,0]∪(2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | (0,$\frac{2}{5}$) | B. | ($\frac{2}{5}$,$\frac{1}{3}$) | C. | ($\frac{2}{5}$,$\frac{1}{2}$) | D. | ($\frac{1}{2}$,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5$\sqrt{2}$ | B. | $\sqrt{41}$ | C. | $\sqrt{53}$ | D. | $\sqrt{45}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [2,+∞) | B. | [$\frac{31}{9}$,5] | C. | (2,+∞) | D. | ($\frac{31}{9}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
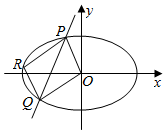 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点为F,上顶点为A,短轴长为2,O为原点,直线AF与椭圆C的另一个交点为B,且△AOF的面积是△BOF的面积的3倍.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点为F,上顶点为A,短轴长为2,O为原点,直线AF与椭圆C的另一个交点为B,且△AOF的面积是△BOF的面积的3倍.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com