练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】设f（x）=|x﹣3|+|x﹣4|．
    （1）求函数 的定义域；
    （2）若存在实数x满足f（x）≤ax﹣1，试求实数a的取值范围．

    【答案】
    （1）解：∵ ，

    它与直线y=2交点的横坐标为 和 ．

    ∴不等式 的定义域为


    （2）解：函数y=ax﹣1的图象是过点（0，﹣1）的直线，

    作出图象，如下图：

    结合图象可知，a取值范围为


    【解析】（1）求出f（x）=|x﹣3|+|x﹣4|与直线y=2交点的横坐标为 和 ，由此能求出不等式 的定义域．（2）函数y=ax﹣1的图象是过点（0，﹣1）的直线，作出图象，结合图象能求出实数a的取值范围．
    【考点精析】掌握绝对值不等式的解法是解答本题的根本，需要知道含绝对值不等式的解法：定义法、平方法、同解变形法，其同解定理有；规律：关键是去掉绝对值的符号．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】从含有两件正品，和一件次品的3件产品中每次任取一件，连续取两次，求取出的两件产品中恰有一件是次品的概率．

    （1）每次取出不放回；

    （2）每次取出后放回．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示，ABCD是一块边长为7米的正方形铁皮，其中ATN是一半径为6米的扇形，已经被腐蚀不能使用，其余部分完好可利用．工人师傅想在未被腐蚀部分截下一个有边落在BC与CD上的长方形铁皮，其中P是弧TN上一点．设，长方形的面积为S平方米．

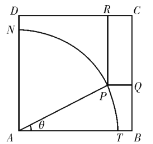
    （1）求关于的函数解析式；

    （2）求的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为了调查喜欢看书是否与性别有关，某校调查小组就“是否喜欢看书”这个问题，在全校随机调研了100名学生.

    （1）完成下列列联表：

    喜欢看书

    不喜欢看书

    合计

    女生

    15

    50

    男生

    25

    合计

    100

    （2）能否在犯错率不超过0.025的前提下认为“喜欢看书与性别有关”.

    附：

    0.15

    0.10

    0.05

    0.025

    0.010

    0.005

    0.001

    2.072

    2.706

    3.841

    5.024

    6.635

    7.879

    10.828

    （参考公式：，其中）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，过点P作圆O的割线PBA与切线PE，E为切点，连接AE、BE，∠APE的平分线与AE、BE分别交于点C、D，其中∠AEB=30°．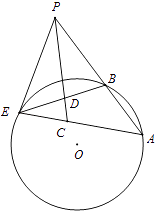

    （1）求证：
    （2）求∠PCE的大小．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在长方体中，，点为的中点．

    （1）求证：直线平面；

    （2）求证：平面平面；

    （3）求直线与平面的夹角．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，过点P作圆O的割线PBA与切线PE，E为切点，连接AE、BE，∠APE的平分线与AE、BE分别交于点C、D，其中∠AEB=30°．

    （1）求证：
    （2）求∠PCE的大小．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在城市旧城改造中，某小区为了升级居住环境，拟在小区的闲置地中规划一个面积为的矩形区域（如图所示），按规划要求：在矩形内的四周安排宽的绿化，绿化造价为200元/，中间区域地面硬化以方便后期放置各类健身器材，硬化造价为100元/.设矩形的长为.

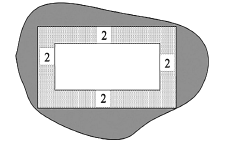
    （1）设总造价（元）表示为长度的函数；

    （2）当取何值时，总造价最低，并求出最低总造价.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）若，证明：当时，；当时，；

    （2）若是的极大值点，求.

    查看答案和解析>>

    同步练习册答案