
| 5×4 |
| 2 |
| 2(1-25) |
| 1-2 |
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| an | 100 | 110 | 120 | 130 | 140 | 150 | 160 | 170 |
| bn | 100 | 102 | 106 | 114 | 130 | 162 | 226 | 354 |


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:高中数学 来源: 题型:
| 1 |
| 3 |
| 1-a |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
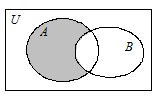 设全集为U=R,集合A={x|(x+3)(x-6)≥0},B={x|log2(x+2)<4}.
设全集为U=R,集合A={x|(x+3)(x-6)≥0},B={x|log2(x+2)<4}. 查看答案和解析>>
科目:高中数学 来源: 题型:
 某简谐运动的图象对应的函数解析式为:y=
某简谐运动的图象对应的函数解析式为:y=| 2 |
| π |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图:港口A北偏东30°方向的C处有一观测站,港口正东方向的B处有一轮船,测得BC为31n mile,该轮船从B处沿正西方向航行20n mile后到D处,测得CD为21n mile.
如图:港口A北偏东30°方向的C处有一观测站,港口正东方向的B处有一轮船,测得BC为31n mile,该轮船从B处沿正西方向航行20n mile后到D处,测得CD为21n mile.查看答案和解析>>
科目:高中数学 来源: 题型:
| a2 |
| a1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com