
【题目】如图,某市郊外景区内一条笔直的公路![]() 经过三个景点
经过三个景点![]() 、
、![]() 、
、![]() ,景区管委会又开发了风景优美的景点
,景区管委会又开发了风景优美的景点![]() ,经测量景点
,经测量景点![]() 位于景点
位于景点![]() 的北偏东
的北偏东![]() 方向
方向![]() 处,位于景点
处,位于景点![]() 的正北方向,还位于景点
的正北方向,还位于景点![]() 的北偏西
的北偏西![]() 方向上,已知
方向上,已知![]() .
.
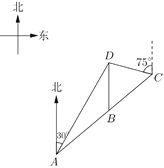
(1)景区管委会准备由景点![]() 向景点
向景点![]() 修建一条笔直的公路,不考虑其他因素,求出这条公路的长;(结果精确到
修建一条笔直的公路,不考虑其他因素,求出这条公路的长;(结果精确到![]() )
)
(2)求景点![]() 与景点
与景点![]() 之间的距离.(结果精确到
之间的距离.(结果精确到![]() )
)
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)过点D作DE⊥AC于点E,过点A作AF⊥DB,交DB的延长线于点F,求DE的问题就可以转化为求∠DBE的度数或三角函数值的问题.
(2)Rt△DCE中根据三角函数就可以求出CD的长.
(1)如图,过点D作DE⊥AC于点E,过点A作AF⊥DB,交DB的延长线于点F
在Rt△DAF中,∠ADF=30°,∴AF![]() AD
AD![]() 8=4,∴DF
8=4,∴DF![]() ;
;
在Rt△ABF中,BF![]() 3,∴BD=DF﹣BF=4
3,∴BD=DF﹣BF=4![]() 3
3
sin∠ABF![]() ,在Rt△DBE中,sin∠DBE
,在Rt△DBE中,sin∠DBE![]() ,
,
∵∠ABF=∠DBE,∴sin∠DBE![]() ,
,
∴DE=BDsin∠DBE![]() (4
(4![]() 3)
3)![]() 3.1(km)
3.1(km)
∴景点D向公路a修建的这条公路的长约是3.1km;
(2)由题意可知∠CDB=75°,由(1)可知sin∠DBE![]() 0.8,所以∠DBE=53°,∴∠DCB=180°﹣75°﹣53°=52°
0.8,所以∠DBE=53°,∴∠DCB=180°﹣75°﹣53°=52°
在Rt△DCE中,sin∠DCE![]() ,∴DC
,∴DC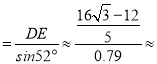 4.0(km)
4.0(km)
∴景点C与景点D之间的距离约为4.0km.


科目:高中数学 来源: 题型:
【题目】已知双曲线 C 经过点 (2,3),它的渐近线方程为 y = ±![]() .椭圆 C1与双曲线 C有相同的焦点,椭圆 C1的短轴长与双曲线 C 的实轴长相等.
.椭圆 C1与双曲线 C有相同的焦点,椭圆 C1的短轴长与双曲线 C 的实轴长相等.
(1)求双曲线 C 和椭圆 C1 的方程;
(2)经过椭圆 C1 左焦点 F 的直线 l 与椭圆 C1 交于 A、B 两点,是否存在定点 D ,使得无论 AB 怎样运动,都有∠ADF = ∠BDF ?若存在,求出 D 点坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,点
,点 在
在![]() 上.
上.
(1) 求椭圆的方程;
(2) 设![]() 分别是椭圆
分别是椭圆![]() 的上、下焦点,过
的上、下焦点,过![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() ,求
,求![]() 的内切圆的半径的最大值.
的内切圆的半径的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解居民的家庭收入情况,某社区组织工作人员从该社区的居民中随机抽取了![]() 户家庭进行问卷调查,经调查发现,这些家庭的月收人在
户家庭进行问卷调查,经调查发现,这些家庭的月收人在![]() 元到
元到![]() 元之间,根据统计数据作出:
元之间,根据统计数据作出:
(1)经统计发现,该社区居民的家庭月收人![]() (单位:百元)近似地服从正态分布
(单位:百元)近似地服从正态分布![]() ,其中
,其中![]() 近似为样本平均数.若
近似为样本平均数.若![]() 落在区间
落在区间![]() 的左侧,则可认为该家庭属“收入较低家庭" ,社区将联系该家庭,咨询收入过低的原因,并采取相应措施为该家庭提供创收途径.若该社区
的左侧,则可认为该家庭属“收入较低家庭" ,社区将联系该家庭,咨询收入过低的原因,并采取相应措施为该家庭提供创收途径.若该社区![]() 家庭月收入为
家庭月收入为![]() 元,试判断
元,试判断![]() 家庭是否属于“收人较低家庭”,并说明原因;
家庭是否属于“收人较低家庭”,并说明原因;
(2)将样本的频率视为总体的概率
①从该社区所有家庭中随机抽取![]() 户家庭,若这
户家庭,若这![]() 户家庭月收人均低于
户家庭月收人均低于![]() 元的概率不小于
元的概率不小于![]() ,求
,求![]() 的最大值;
的最大值;
②在①的条件下,某生活超市赞助了该社区的这次调查活动,并为这次参与调在的家庭制定了贈送购物卡的活动,贈送方式为:家庭月收入低于![]() 的获赠两次随机购物卡,家庭月收入不低于
的获赠两次随机购物卡,家庭月收入不低于![]() 的获赠一次随机购物卡;每次赠送的购物卡金额及对应的概率分别为:
的获赠一次随机购物卡;每次赠送的购物卡金额及对应的概率分别为:
赠送购物卡金额(单位:元) |
|
|
|
概率 |
|
|
|
则![]() 家庭预期获得的购物卡金额为多少元?(结果保留整数)
家庭预期获得的购物卡金额为多少元?(结果保留整数)

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学为丰富教职工生活,在元旦期间举办趣味投篮比赛,设置A,B两个投篮位置,在A点投中一球得1分,在B点投中一球得2分,规则是:每人按先A后B的顺序各投篮一次(计为投篮两次),教师甲在A点和B点投中的概率分别为![]() 和
和![]() ,且在A,B两点投中与否相互独立.
,且在A,B两点投中与否相互独立.
(1)若教师甲投篮两次,求教师甲投篮得分0分的概率
(2)若教师乙与教师甲在A,B投中的概率相同,两人按规则投篮两次,求甲得分比乙高的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中![]() ,以原点
,以原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系,直线
轴正半轴为极轴,建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() 的参数方程为:
的参数方程为: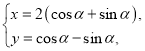 (
(![]() 为参数),
为参数),![]() ,
,![]() 为直线
为直线![]() 上距离为
上距离为![]() 的两动点,点
的两动点,点![]() 为曲线
为曲线![]() 上的动点且不在直线
上的动点且不在直线![]() 上.
上.
(1)求曲线![]() 的普通方程及直线
的普通方程及直线![]() 的直角坐标方程.
的直角坐标方程.
(2)求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某污水处理厂要在一个矩形污水处理池(ABCD)的池底水平铺设污水净化管道(管道构成Rt△FHE,H是直角项点)来处理污水.管道越长,污水净化效果越好.设计要求管道的接口H是AB的中点,E,F分别落在线段BC,AD上.已知AB=20米,AD=![]() 米,记∠BHE=
米,记∠BHE=![]() .
.

(1)试将污水净化管道的长度L表示为![]() 的函数,并写出定义域;
的函数,并写出定义域;
(2)当![]() 取何值时,污水净化效果最好?并求出此时管道的长度L.
取何值时,污水净化效果最好?并求出此时管道的长度L.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ;
;
(1)当![]() 时,若
时,若![]() ,求
,求![]() 的取值范围;
的取值范围;
(2)若定义在![]() 上奇函数
上奇函数![]() 满足
满足![]() ,且当
,且当![]() 时,
时, ![]() ,
,
求![]() 在
在![]() 上的反函数
上的反函数![]() ;
;
(3)对于(2)中的![]() ,若关于
,若关于![]() 的不等式
的不等式 在
在![]() 上恒成立,求实
上恒成立,求实
数![]() 的取值范围;
的取值范围;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com