
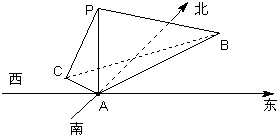
 在海岛A上有一座海拔1千米的山,山顶设有一个观察站P,上午9时测得一轮船在海岛北偏东30°,俯角为30°的B处,匀速直行10分钟后,测得该船位于海岛北偏西60°,俯角为45°的C处.从C处开始,该船航向改为正南方向,且速度大小不变,则该船经过10分钟后离开A点的距离为( )
在海岛A上有一座海拔1千米的山,山顶设有一个观察站P,上午9时测得一轮船在海岛北偏东30°,俯角为30°的B处,匀速直行10分钟后,测得该船位于海岛北偏西60°,俯角为45°的C处.从C处开始,该船航向改为正南方向,且速度大小不变,则该船经过10分钟后离开A点的距离为( )| A、1千米 | ||
| B、2千米 | ||
C、
| ||
D、2
|
| 1 |
| 2 |
| 3 |
| 3 |


 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:高中数学 来源: 题型:
| A、a<b | B、a>b |
| C、a≤b | D、a≥b |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||
| B、2 | ||
C、
| ||
D、
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、20种 | B、25种 |
| C、45种 | D、75种 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com