
已知函数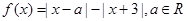 .
.
(1)当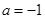 时,解不等式
时,解不等式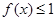 ;
;
(2)若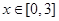 时,
时,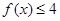 ,求a的取值范围.
,求a的取值范围.
(1) ;(2)[-7,7].
;(2)[-7,7].
解析试题分析:本题主要考查绝对值不等式的解法、不等式恒成立等基础知识,考查学生分析问题解决问题的能力、转化能力、计算能力.第一问,先把a=-1代入,先写出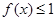 的解析式,利用零点分段法去掉绝对值,解不等式组,得到不等式的解集;第二问,在已知的
的解析式,利用零点分段法去掉绝对值,解不等式组,得到不等式的解集;第二问,在已知的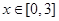 范围内
范围内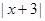 的绝对值可去掉,解绝对值不等式,使之转化成2个恒成立.
的绝对值可去掉,解绝对值不等式,使之转化成2个恒成立.
试题解析:(1)当a=-1时,不等式为|x+1|-|x+3|≤1.
当x≤-3时,不等式化为-(x+1)+(x+3)≤1,不等式不成立;
当-3<x<-1时,不等式化为-(x+1)-(x+3)≤1,解得 ;
;
当x≥-1时,不等式化为(x+1)-(x+3)≤1,不等式必成立.
综上,不等式的解集为 . 5分
. 5分
(2)当x∈[0,3]时,f(x)≤4即|x-a|≤x+7,
由此得a≥-7且a≤2x+7.
当x∈[0,3]时,2x+7的最小值为7,
所以a的取值范围是[-7,7]. 10分
考点:绝对值不等式的解法、不等式恒成立.


科目:高中数学 来源: 题型:解答题
已知函数f(x)=|x+a|+|x-2|.
(1)当a=-3时,求不等式f(x)≥3的解集;
(2)若f(x)≤|x-4|的解集包含[1,2],求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com