解关于x的不等式：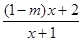
≤
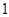
详见解析
解析试题分析：首先移项化简，得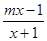
≥
，对m进行分类讨论，分别讨论m=0，m>0，m<0的情形，即可得到结果．．
试题解析：解：原不等式化为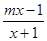≥ (1分)
①当m=0时，原不等式化为－x-1>0,解集为（-∞，-1） (3分)
②当m>0时，原不等式化为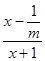
≥，又
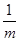> -1
∴原不等式的解集为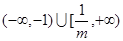
(5分)
③当m<0时，原不等式化为≤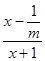
当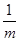< -1即-1<m<0时，所以原不等式的解集为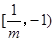
当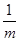=-1即 m=-1时，所以原不等式的解集为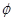
当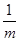> -1即m<-1时，所以原不等式的解集为
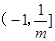(11分)
综上所述，当m=0时，原不等式解集为（-∞，-1）
当m>0时，原不等式的解集为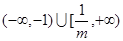
当 1<m<0时，原不等式的解集为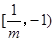
当 m=-1时，原不等式的解集为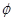
当m<-1时，原不等式的解集为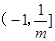
考点：1．分式不等式的解法；2．分类讨论思想．
期末冲刺100分创新金卷完全试卷系列答案科目：高中数学 来源： 题型：解答题
设二次函数f(x)＝ax2＋bx＋c，函数F(x)＝f(x)－x的两个零点为m，n(m<n)．
(1)若m＝－1，n＝2，求不等式F(x)>0的解集；
(2)若a>0，且0<x<m<n<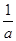
，比较f(x)与m的大小．
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
已知不等式(2＋x)(3－x)≥0的解集为A，函数f(x)＝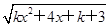
(k<0)的定义域为B.
(1)求集合A；
(2)若集合B中仅有一个元素，试求实数k的值；
(3)若B?A，试求实数k的取值范围．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
的解集为
，则实数a的取值范围是 
．
时，求不等式
的解集；
存在实数解，求实数
的取值范围.
＋1.
.
时，解不等式
；
时，
，求a的取值范围.
．
的解集为
，求实数a的值； 
使
成立，求实数
的取值范围． 
其中
.