
【题目】下列关于命题的说法错误的是( )
A.命题“若![]() ,则
,则![]() ”的逆否命题为“若
”的逆否命题为“若![]() ,则
,则![]() ”
”
B.“![]() ”是“函数
”是“函数![]() 在区间
在区间![]() 上为增函数”的充分不必要条件
上为增函数”的充分不必要条件
C.扇形的周长为![]() ,则当其圆心角的弧度数为
,则当其圆心角的弧度数为![]() 时,其面积最大
时,其面积最大
D.若扇形的周长为![]() ,面积为
,面积为![]() ,则该扇形的圆心角的弧度数为
,则该扇形的圆心角的弧度数为![]() 或
或![]()
【答案】D
【解析】
根据逆否命题与原命题的关系判断选项A中命题的正误;根据函数![]() 的单调性求出实数
的单调性求出实数![]() 的取值范围,可判断选项B中命题的正误;设扇形的半径为
的取值范围,可判断选项B中命题的正误;设扇形的半径为![]() ,利用二次函数求出扇形面积的最大值,求出
,利用二次函数求出扇形面积的最大值,求出![]() 的值,可判断选项C中命题的正误;根据扇形圆心角弧度数小于
的值,可判断选项C中命题的正误;根据扇形圆心角弧度数小于![]() 可判断D选项中命题的正误.
可判断D选项中命题的正误.
对于A选项,命题“若![]() ,则
,则![]() ”的逆否命题为“若
”的逆否命题为“若![]() ,则
,则![]() ”,该命题正确;
”,该命题正确;
对于B选项,若函数![]() 在区间
在区间![]() 上为增函数,则
上为增函数,则![]() ,所以,“
,所以,“![]() ”是“函数
”是“函数![]() 在区间
在区间![]() 上为增函数”的充分不必要条件,该命题正确;
上为增函数”的充分不必要条件,该命题正确;
对于C选项,设扇形的半径为![]() ,则扇形的弧长为
,则扇形的弧长为![]() ,扇形的面积为
,扇形的面积为![]() ,
,
当![]() 时,扇形圆心角的弧度数为
时,扇形圆心角的弧度数为![]() 时,扇形的面积最大,该命题正确;
时,扇形的面积最大,该命题正确;
对于D选项,由于扇形的弧度数的范围是![]() ,且
,且![]() ,该命题错误.
,该命题错误.
故选:D.


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,平面ABCD平面PAD,
中,平面ABCD平面PAD,![]() ,
,![]() ,
,![]() ,
,![]() ,E是PD的中点.
,E是PD的中点.

![]() 证明:
证明:![]() ;
;
![]() 设
设![]() ,点M在线段PC上且异面直线BM与CE所成角的余弦值为
,点M在线段PC上且异面直线BM与CE所成角的余弦值为![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() ,
,![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的坐标方程为
的坐标方程为![]() ,若直线
,若直线![]() 与曲线
与曲线![]() 相切.
相切.
(1)求曲线![]() 的极坐标方程;
的极坐标方程;
(2)在曲线![]() 上取两点
上取两点![]() 、
、![]() 于原点
于原点![]() 构成
构成![]() ,且满足
,且满足![]() ,求面积
,求面积![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() ,下述四个结论:
,下述四个结论:
①![]() 是偶函数;
是偶函数;
②![]() 的最小正周期为
的最小正周期为![]() ;
;
③![]() 的最小值为0;
的最小值为0;
④![]() 在
在![]() 上有3个零点
上有3个零点
其中所有正确结论的编号是( )
A.①②B.①②③C.①③④D.②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】里氏震级M的计算公式为:M=lgA﹣lgA0,其中A是测震仪记录的地震曲线的最大振幅,是相应的标准地震的振幅,假设在一次地震中,测震仪记录的最大振幅是1000,此时标准地震的振幅A0为0.001,则此次地震的震级为 级;9级地震的最大的振幅是5级地震最大振幅的 倍.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,圆
中,圆![]() 的参数方程
的参数方程![]() (
(![]() 为参数).以
为参数).以![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系.
轴的非负半轴为极轴建立极坐标系.
(1)求圆![]() 的极坐标方程;
的极坐标方程;
(2)直线![]() 的极坐标方程是
的极坐标方程是![]() ,射线
,射线![]() 与圆
与圆![]() 的交点为
的交点为![]() ,
,![]() ,与直线
,与直线![]() 的交点为
的交点为![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】第![]() 届冬奥会将于
届冬奥会将于![]() 年在中国北京和张家口举行,为宣传冬奥会,让更多的人了解、喜爱冰雪项目,某大学举办了冬奥会知识竞赛,并从中随机抽取了
年在中国北京和张家口举行,为宣传冬奥会,让更多的人了解、喜爱冰雪项目,某大学举办了冬奥会知识竞赛,并从中随机抽取了![]() 名学生的成绩,绘制成如图所示的频率分布直方图.
名学生的成绩,绘制成如图所示的频率分布直方图.
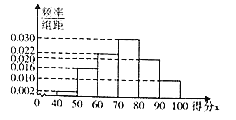
(Ⅰ)试根据频率分布直方图估计这![]() 名学生的平均成绩(同一组数据用该组区间的中点值代替);
名学生的平均成绩(同一组数据用该组区间的中点值代替);
(Ⅱ)若采用分层抽样的方法从![]() 、
、![]() 这两个分数段中抽取
这两个分数段中抽取![]() 人,求从这两个分数段中应分别抽取多少人?
人,求从这两个分数段中应分别抽取多少人?
(Ⅲ)从(Ⅱ)中抽取的![]() 人中随机抽取
人中随机抽取![]() 人到某社区开展冬奥会宜传活动,求抽取的
人到某社区开展冬奥会宜传活动,求抽取的![]() 人成绩均在
人成绩均在![]() 中的概率.
中的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com