
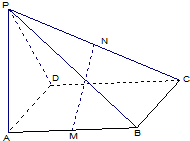
 如图,PA⊥矩形ABCD所在的平面,M、N分别是AB、PC的中点,PA=AD=a,AB=2a.
如图,PA⊥矩形ABCD所在的平面,M、N分别是AB、PC的中点,PA=AD=a,AB=2a.分析 (1)取PD的中点E,连结AE、EN,证明四边形AMNE是平行四边形,可得MN∥AE,利用线面平行的判定,即可得出结论.
(2)由线面垂直得PA⊥CD,由矩形性质得AD⊥CD,由此能证明CD⊥MN.
(3)连接AC,PA⊥矩形ABCD所在的平面,所以∠PCA为PC与平面ABCD所成角.
解答 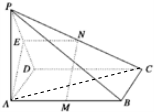 (1)证明:取PD 的中点E,连接AE、EN,
(1)证明:取PD 的中点E,连接AE、EN,
则有EN=$\frac{1}{2}CD$=$\frac{1}{2}AB$=AM,EN∥CD∥AB∥AM,
故AMNE 是平行四边形,
∴MN∥AE,
∵AE?平面PAD,MN?平面PAD,
∴MN∥平面PAD.
(2)证明:∵PA⊥平面ABCD,
∴PA⊥AB,又AD⊥AB,
∴AB⊥平面PAD,
∴AB⊥AE,即AB⊥MN,
又CD∥AB,
∴MN⊥CD.
(3)解:连接AC,PA⊥矩形ABCD所在的平面,
所以∠PCA为PC与平面ABCD所成角,
AB=2a,BC=a,∴AC=$\sqrt{5}$a,PA=a,
∴tan∠PCA=$\frac{PA}{AC}$=$\frac{\sqrt{5}}{5}$.
点评 本题考查线面平行的证明,考查线线垂直的证明,考查线面角,熟练掌握空间直线与平面平行及垂直的判定和性质是解答本题的关键.


科目:高中数学 来源: 题型:解答题
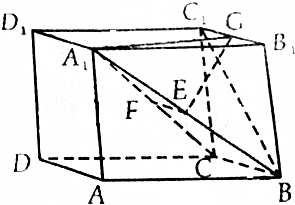 如图,已知直平行六面体ABCD-A1B1C1D1的底面边长均为2a,侧棱长均为a,∠ABC=60°,E、F、G分别是A1B、A1C、B1C1的中点.
如图,已知直平行六面体ABCD-A1B1C1D1的底面边长均为2a,侧棱长均为a,∠ABC=60°,E、F、G分别是A1B、A1C、B1C1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 0 | B. | $\frac{\sqrt{3}}{3}$ | C. | $\sqrt{3}$ | D. | -$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 四棱锥P-ABCD中,AB∥CD,AB⊥BC,AB=BC=2CD=2,AP=PB=3,PC=$\sqrt{5}$.
四棱锥P-ABCD中,AB∥CD,AB⊥BC,AB=BC=2CD=2,AP=PB=3,PC=$\sqrt{5}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com