
分析 (Ⅰ)由题意可得|x-1|+|x-2|小于或等于$\frac{|a+b|+|a-b|}{|a|}$的最小值,而$\frac{|a+b|+|a-b|}{|a|}$的最小值等于2,故x的范围即为不等式|x-1|+|x-2|≤2的解,根据数轴上的$\frac{1}{2}$、$\frac{5}{2}$对应点到1和2对应点的距离之和等于2,可得不等式的解集.
(Ⅱ)$\frac{1}{3}$×($\sqrt{3x+1}$+$\sqrt{3y+1}$+$\sqrt{3z+1}$)≤$\sqrt{\frac{3x+1+3y+1+3z+1}{3}}$=$\sqrt{2}$,即可得出结论.
解答 解:(Ⅰ)由题知,|x-1|+|x-2|≤$\frac{|a+b|+|a-b|}{|a|}$恒成立,
故|x-1|+|x-2|小于或等于$\frac{|a+b|+|a-b|}{|a|}$的最小值.
∵|a+b|+|a-b|≥|a+b+a-b|=2|a|,当且仅当 (a+b)(a-b)≥0 时取等号,
∴$\frac{|a+b|+|a-b|}{|a|}$的最小值等于2,∴x的范围即为不等式|x-1|+|x-2|≤2的解.
由于|x-1|+|x-2|表示数轴上的x对应点到1和2对应点的距离之和,
又由于数轴上的$\frac{1}{2}$、$\frac{5}{2}$对应点到1和2对应点的距离之和等于2,
故不等式的解集为[$\frac{1}{2}$,$\frac{5}{2}$].
(Ⅱ)$\frac{1}{3}$×($\sqrt{3x+1}$+$\sqrt{3y+1}$+$\sqrt{3z+1}$)≤$\sqrt{\frac{3x+1+3y+1+3z+1}{3}}$=$\sqrt{2}$.
∴$\sqrt{3x+1}$+$\sqrt{3y+1}$+$\sqrt{3z+1}$≤3$\sqrt{2}$≠5,所以不存在这样的x,y,z满足条件.
点评 本题考查绝对值的意义,绝对值不等式的解法,考查基本不等式的运用,判断|x-1|+|x-2|表示数轴上的x对应点到1和2对应点的距离之和,是解题的关键.


 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案科目:高中数学 来源: 题型:选择题
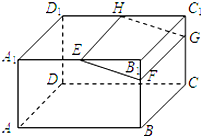 如图,在长方体ABCD-A1B1C1D1中,E,H分别是棱A1B1,D1C1上的动点(点E与B1不重合),且EH∥A1D1,过EH的动平面与棱BB1,CC1相交,交点分别为F,G.设AB=2AA1=2a,B1E+B1F=2a.在长方体ABCD-A1B1C1D1内随机选取一点,则该点取自于几何体A1ABFE-D1DCGH内的概率的最小值为( )
如图,在长方体ABCD-A1B1C1D1中,E,H分别是棱A1B1,D1C1上的动点(点E与B1不重合),且EH∥A1D1,过EH的动平面与棱BB1,CC1相交,交点分别为F,G.设AB=2AA1=2a,B1E+B1F=2a.在长方体ABCD-A1B1C1D1内随机选取一点,则该点取自于几何体A1ABFE-D1DCGH内的概率的最小值为( )| A. | $\frac{11}{12}$ | B. | $\frac{3}{4}$ | C. | $\frac{13}{16}$ | D. | $\frac{7}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
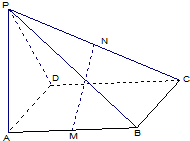 如图,PA⊥矩形ABCD所在的平面,M、N分别是AB、PC的中点,PA=AD=a,AB=2a.
如图,PA⊥矩形ABCD所在的平面,M、N分别是AB、PC的中点,PA=AD=a,AB=2a.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com