练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    甲、乙、丙3位志愿者安排在周一至周五的5天中参加某项志愿者活动，要求每人参加一天且每天至多安排一人，并要求甲安排在另外两位前面，不同的安排方法共有多少种？

     

    20(种)

    【解析】

    【解析】
    甲排周一时，乙有4种排法，丙则有3种排法，共有4×3＝12(种)；

    甲排周二时，乙有3种排法，丙有2种排法，共3×2＝6(种)；

    甲排周三时，乙有2种排法，丙有1种排法，共2×1＝2(种)．

    由分类计数原理得：共有12＋6＋2＝20(种)．

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2015届苏教版选修2-3高二数学双基达标1.5练习卷（解析版） 题型：填空题

    6的展开式中，x3的系数等于________．

     

    查看答案和解析>>

    科目：高中数学 来源：2015届苏教版选修2-3高二数学双基达标1.2练习卷（解析版） 题型：填空题

    安排5名选手的演讲顺序时，要求某名选手不第一个出场，另一名选手不最后一个出场，则不同排法的总数是________(用数字作答)．

     

    查看答案和解析>>

    科目：高中数学 来源：2015届苏教版选修2-3高二数学双基达标1.1练习卷（解析版） 题型：解答题

    将红、黄、绿、黑四种不同的颜色涂入如图中的五个区域内，要求相邻的两个区域的颜色都不相同，则有多少种不同的涂色方法？

     

     

    查看答案和解析>>

    科目：高中数学 来源：2015届苏教版选修2-3高二数学双基达标1.1练习卷（解析版） 题型：填空题

    “渐升数”是指每个数字比它左边的数字大的正整数(如1 458)，若把四位“渐升数”按从小到大的顺序排列，则第30个数为________．

     

    查看答案和解析>>

    科目：高中数学 来源：2015届苏教版选修2-3高二数学双基达标1.1练习卷（解析版） 题型：填空题

    若a，b∈N*，且a＋b≤5，则复数a＋bi的个数为______．

     

    查看答案和解析>>

    科目：高中数学 来源：2015届福建省龙岩市高二上学期教学质量检查理科数学试卷（解析版） 题型：解答题

    设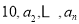是各项均不为零的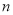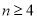（）项等差数列，且公差.

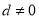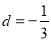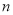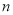    （1）若,且该数列前项和最大，求的值；

    （2）若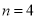,且将此数列删去某一项后得到的数列（按原来的顺序）是等比数列，求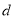的值；

    （3）若该数列中有一项是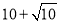，则数列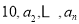中是否存在不同三项（按原来的顺序）为等比数列？请说明理由.

     

    查看答案和解析>>

    科目：高中数学 来源：2015届福建省龙岩市高二上学期教学质量检查理科数学试卷（解析版） 题型：选择题

    若椭圆的焦点分别为，弦过点，则的周长为

    A． B． C． 8 D．

     

    查看答案和解析>>

    科目：高中数学 来源：2015届福建省高二下学期期末考试理科数学试卷（解析版） 题型：选择题

    下列四组中的f（x），g（x），表示同一个函数的是（ ）．

    A．f（x）＝1，g（x）＝x0 B．f（x）＝x－1，g（x）＝－1

    C．f（x）＝x2，g（x）＝（）4 D．f（x）＝x3，g（x）＝

     

    查看答案和解析>>

    同步练习册答案