
设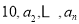 是各项均不为零的
是各项均不为零的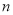 (
(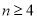 )项等差数列,且公差
)项等差数列,且公差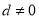 .
.
(1)若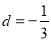 ,且该数列前
,且该数列前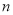 项和
项和 最大,求
最大,求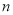 的值;
的值;
(2)若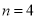 ,且将此数列删去某一项后得到的数列(按原来的顺序)是等比数列,求
,且将此数列删去某一项后得到的数列(按原来的顺序)是等比数列,求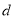 的值;
的值;
(3)若该数列中有一项是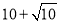 ,则数列
,则数列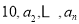 中是否存在不同三项(按原来的顺序)为等比数列?请说明理由.
中是否存在不同三项(按原来的顺序)为等比数列?请说明理由.
(1)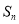 取最大时
取最大时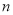 的值为30或31;(2)
的值为30或31;(2)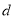 的值为
的值为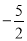 或10
或10
【解析】
试题分析:(1)由等差数列前n项和的二次函数性质求解
(2)分类讨论思想,依次分删去第一项、第二项、第三项、第四项后成等比数列求解;
(3)考虑反证法
试题解析:(1)解法一:由已知得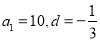
∴
∵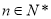 ∴
∴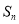 取最大时
取最大时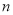 的值为30或31.
的值为30或31.
解法二:由已知得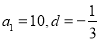 ∴
∴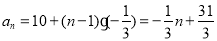 .
.
若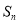 取最大,则只需
取最大,则只需 即
即 解得
解得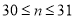 .
.
∵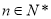 ∴当
∴当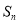 取最大时
取最大时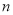 的值分别是30或31.
的值分别是30或31.
(2)当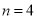 时,该数列的前4项可设为10、
时,该数列的前4项可设为10、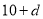 、
、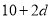 、
、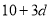 .
.
若删去第一项10,则由题意得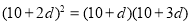 ,解得
,解得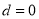 ,不符合题意.
,不符合题意.
若删去第二项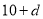 ,则由题意得
,则由题意得 解得
解得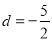 ,符合题意.
,符合题意.
若删去第三项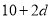 ,则由题意得
,则由题意得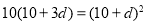 解得
解得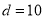 ,符合题意.
,符合题意.
若删去第四项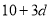 ,则由题意得
,则由题意得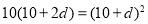 解得
解得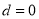 ,不符合题意.
,不符合题意.
综上所述,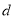 的值为
的值为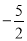 或10.
或10.
(3)设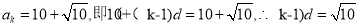
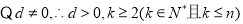
设该数列存在不同的三项 成等比数列,则
成等比数列,则
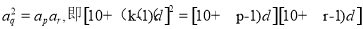 ,化简得
,化简得
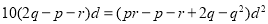
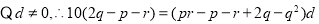
又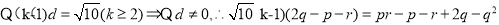
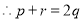 将
将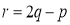 代入
代入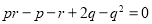 得
得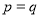 这与题设
这与题设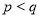 矛盾
矛盾
故该数列不存在不同三项(按原来的顺序)为等比数列.
考点:等差数列的定义及性质,等比数列的定义及性质


 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:高中数学 来源:2015届苏教版选修2-3高二数学双基达标1.4练习卷(解析版) 题型:填空题
某外商计划在5个候选城市投资3个不同的项目,且在同一个城市投资的项目不超过2个,则该外商不同的投资方案有________.
查看答案和解析>>
科目:高中数学 来源:2015届苏教版选修2-3高二数学双基达标1.2练习卷(解析版) 题型:解答题
解下列方程或不等式.
(1)3?A8x=4?A9x-1;(2)Ax-22+x≥2.
查看答案和解析>>
科目:高中数学 来源:2015届苏教版选修2-3高二数学双基达标1.1练习卷(解析版) 题型:解答题
甲、乙、丙3位志愿者安排在周一至周五的5天中参加某项志愿者活动,要求每人参加一天且每天至多安排一人,并要求甲安排在另外两位前面,不同的安排方法共有多少种?
查看答案和解析>>
科目:高中数学 来源:2015届苏教版选修2-3高二数学双基达标1.1练习卷(解析版) 题型:填空题
在一宝宝“抓周”的仪式上,他面前摆着4件学习用品,3件生活用品,4件娱乐用品,若他只抓其中的一件物品,则他抓的结果有________种.
查看答案和解析>>
科目:高中数学 来源:2015届福建省龙岩市高二上学期教学质量检查理科数学试卷(解析版) 题型:填空题
设非空集合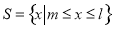 满足:当
满足:当 时,有
时,有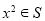 .给出如下命题:①若
.给出如下命题:①若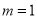 ,
,
则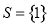 ;②若
;②若 ,则
,则 ;③若
;③若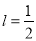 ,则
,则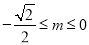 ;④若
;④若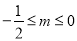 ,
,
则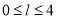 .其中所有正确命题的序号是.
.其中所有正确命题的序号是.
查看答案和解析>>
科目:高中数学 来源:2015届福建省龙岩市高二上学期教学质量检查理科数学试卷(解析版) 题型:选择题
已知对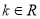 ,直线
,直线 与椭圆
与椭圆 恒有公共点,则实数
恒有公共点,则实数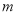 的取值范围是
的取值范围是
A.(0, 1) B.(0,5) C.[1,5) D.[1,5)∪(5,+∞)
查看答案和解析>>
科目:高中数学 来源:2015届福建省高二上学期期中考试理科数学试卷(解析版) 题型:选择题
已知Ω={(x,y)|x+y≤6,x≥0,y≥0},A={(x,y)|x≤4,y≥0,x-2y≥0},若向区域Ω上随机投一点P,则点P落入区域A的概率为( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com