
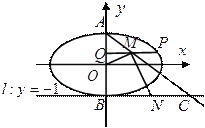
【题目】如图,已知中心在原点,焦点在![]() 轴上的椭圆的一个焦点为
轴上的椭圆的一个焦点为![]() ,
, 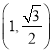 是椭圆上的一个点.
是椭圆上的一个点.
(1)求椭圆的标准方程;
(2)设椭圆的上、下顶点分别为![]() ,
, ![]() (
(![]() )是椭圆上异于
)是椭圆上异于![]() 的任意一点,
的任意一点, ![]() 轴,
轴, ![]() 为垂足,
为垂足, ![]() 为线段
为线段![]() 中点,直线
中点,直线![]() 交直线
交直线![]() 于点
于点![]() ,
, ![]() 为线段
为线段![]() 的中点,如果
的中点,如果![]() 的面积为
的面积为![]() ,求
,求![]() 的值.
的值.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】一个多面体的直观图和三视图如图,M是A1B的中点,N是棱B1C1上的任意一点(含顶点). 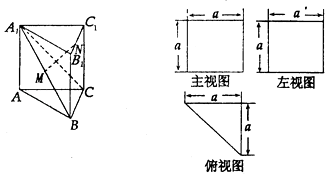
①当点N是棱B1C1的中点时,MN∥平面ACC1A1;
②MN⊥A1C;
③三棱锥N﹣A1BC的体积为VN﹣A ![]() BC=
BC= ![]() a3;
a3;
④点M是该多面体外接球的球心.
其中正确的是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题p:方程 ![]() =1表示焦点在y轴上的椭圆;命题q:双曲线
=1表示焦点在y轴上的椭圆;命题q:双曲线 ![]() ﹣
﹣ ![]() =1的离心率e∈(1,2).若命题p、q有且只有一个为真,求m的取值范围.
=1的离心率e∈(1,2).若命题p、q有且只有一个为真,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 是空间两条直线,
是空间两条直线, ![]() 是空间两个平面,则下列命题中不正确的是( )
是空间两个平面,则下列命题中不正确的是( )
A. 当![]() 时,“
时,“![]() ”是“
”是“![]() ”的充要条件
”的充要条件
B. 当![]() 时,“
时,“![]() ”是“
”是“![]() ”的充分不必要条件
”的充分不必要条件
C. 当![]() 时,“
时,“![]() ”是“
”是“![]() ”的必要不充分条件
”的必要不充分条件
D. 当![]() 时,“
时,“![]() ”是“
”是“![]() ”的充分不必要条件
”的充分不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥A﹣BCD中,BC=DC=AB=AD= ![]() ,BD=2,平面ABD⊥平面BCD,O为BD中点,点P,Q分别为线段AO,BC上的动点(不含端点),且AP=CQ,则三棱锥P﹣QCO体积的最大值为 .
,BD=2,平面ABD⊥平面BCD,O为BD中点,点P,Q分别为线段AO,BC上的动点(不含端点),且AP=CQ,则三棱锥P﹣QCO体积的最大值为 . 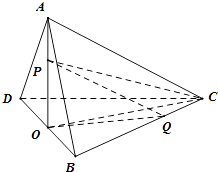
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知单位圆O上的两点A,B及单位圆所在平面上的一点P,满足 ![]() =m
=m ![]() +
+ ![]() (m为常数).
(m为常数). 
(1)如图,若四边形OABP为平行四边形,求m的值;
(2)若m=2,求| ![]() |的取值范围.
|的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若椭圆 ![]() +
+ ![]() =1的焦点在x轴上,过点(1,
=1的焦点在x轴上,过点(1, ![]() )作圆x2+y2=1的切线,切点分别为A,B,直线AB恰好经过椭圆的右焦点和上顶点,则椭圆方程是 .
)作圆x2+y2=1的切线,切点分别为A,B,直线AB恰好经过椭圆的右焦点和上顶点,则椭圆方程是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com