
【题目】设数列{an}的前n项和为Sn . 若对任意正整数n,总存在正整数m,使得Sn=am , 则称{an}是“H数列”.
(1)若数列{an}的前n项和Sn=2n(n∈N*),证明:{an}是“H数列”;
(2)设{an}是等差数列,其首项a1=1,公差d<0.若{an}是“H数列”,求d的值.
【答案】
(1)证明:当n=1时,a1=S1=2,
当n≥2时,an=Sn﹣Sn﹣1=2n﹣2n﹣1=2n﹣1,
所以 ![]() ,
,
所以对任意的n∈N*, ![]() 是数列{an}中的第n+1项,
是数列{an}中的第n+1项,
因此数列{an}是“H数列”
(2)解:依题意,an=1+(n﹣1)d, ![]() ,
,
若{an}是“H数列”,则对任意的n∈N*,都存在k∈N*使得ak=Sn,
即1+(k﹣1)d= ![]() ,
,
所以 ![]() ,
,
又因为k∈N*, ![]() ,
,
所以对任意的n∈N*, ![]() ,且d<0,
,且d<0,
所以d=﹣1.
【解析】(1)由已知得 ![]() ,由此能证明数列{an}是“H数列”.(2)依题意,an=1+(n﹣1)d,
,由此能证明数列{an}是“H数列”.(2)依题意,an=1+(n﹣1)d, ![]() ,若{an}是“H数列”,则1+(k﹣1)d=
,若{an}是“H数列”,则1+(k﹣1)d= ![]() ,由此能求出d的值.
,由此能求出d的值.
【考点精析】通过灵活运用数列的通项公式,掌握如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式即可以解答此题.


科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 中,底面
中,底面![]() 为梯形,
为梯形, ![]() 底面
底面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.

(1)求证:平面![]()
![]() 平面
平面![]() ;
;
(2)设![]() 为
为![]() 上的一点,满足
上的一点,满足![]() ,若直线
,若直线![]() 与平面
与平面![]() 所成角的正切值为
所成角的正切值为![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知四棱锥P﹣ABCD的底面是矩形,侧面PAB是正三角形,且平面PAB⊥平面ABCD,E是PA的中点,AC与BD的交点为M. 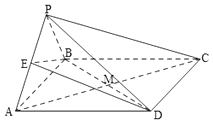
(1)求证:PC∥平面EBD;
(2)求证:BE⊥平面AED.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分13分)设关于![]() 的一元二次方程
的一元二次方程![]()
![]()
![]()
![]()
![]()
![]()
![]() (
(![]() )有两根
)有两根![]() 和
和![]() ,且满足
,且满足![]() .
.
(1)试用![]() 表示
表示![]() ;
;
(2)求证:数列![]() 是等比数列;
是等比数列;
(3)当![]() 时,求数列
时,求数列![]() 的通项公式,并求数列
的通项公式,并求数列![]() 的前
的前![]() 项和
项和![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , 且满足Sn=2an+n(n∈N*).
(1)求证数列{an﹣1}是等比数列,并求数列{an}的通项公式;
(2)若bn=log2(﹣an+1),求数列{ ![]() }的前n项和Tn .
}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=|x﹣a|+|x﹣5|.
(1)当a=1时,求f(x)的最小值;
(2)如果对任意的实数x,都有f(x)≥1成立,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com