已知函数f(x)＝ax2＋bx＋1(a，b为实数)，x∈R，且F(x)＝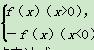
(1)若f(－1)＝0，且函数f(x)的值域为[0，＋∞)，求F(x)的表达式；
(2)在(1)的条件下，当x∈[－2，2]时，g(x)＝f(x)－kx是单调函数，求实数k的取值范围；
(3)设m·n<0，m＋n>0，a>0，且f(x)为偶函数，判断F(m)＋F(n)能否大于零．
科目：高中数学 来源： 题型：
已知函数f(x)＝ex－e－x，g(x)＝ex＋e－x(e＝2.718 28…)．
(1)求[f(x)]2－[g(x)]2的值；
(2)若f(x)f(y)＝4，g(x)g(y)＝8，求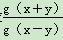
的值．
查看答案和解析>>
科目：高中数学 来源： 题型：
如图K101所示，函数f(x)的图像是曲线OAB，其中点O，A，B的坐标分别为(0，0)，(1，2)，(3，1)，则
＝( )
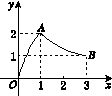
图K101
A．1 B．2 C．0 D.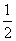
查看答案和解析>>
科目：高中数学 来源： 题型：
某单位拟建一个扇环形状的花坛(如图K125所示)，该扇环是由以点O为圆心的两个同心圆弧和延长后通过点O的两条直线段围成．按设计要求扇环的周长为30米，其中大圆弧所在圆的半径为10米．设小圆弧所在圆的半径为x米，圆心角为θ(弧度)．
(1)求θ关于x的函数关系式；
(2)已知对花坛的边缘(实线部分)进行装饰时，直线部分的装饰费用为4元/米，弧线部分的装饰费用为9元/米．设花坛的面积与装饰总费用之比为y，求y关于x的函数关系式，并求出x为何值时，y取得最大值．
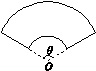
图K125
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
(a≠0)在同一坐标系中的图像可能是( )
＝________．