
分析 由题意知每名谋士对事情作出正确判断的概率为0.7,每名谋士对事情作出正确判断是相互独立的,按按多数人的意见作出决策意见作出决策,即有5,6,7,8,9同意,根据独立重复试验的概率公式写出结果.
解答 解:由题意知每名谋士对事情作出正确判断的概率为0.7,每名谋士对事情作出正确判断是相互独立的,
按按多数人的意见作出决策意见作出决策,即有5,6,7,8,9同意,
作出正确决策的概率P=C950.75(1-0.7)4+C960.76(1-0.7)3+C970.77(1-0.7)2+C980.78(1-0.7)+C990.79(1-0.7)0≈0.9012>0.9,
故这句俗语是有道理
点评 本题考查运用概率知识解决实际问题的能力,注意满足独立重复试验的条件,解题过程中判断概率的类型是难点也是重点,这种题目高考必考,应注意解题的格式.


 特高级教师点拨系列答案
特高级教师点拨系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\sqrt{5}$,2$\sqrt{5}$) | B. | (2$\sqrt{5}$,$\sqrt{5}$) | C. | (-$\sqrt{5}$,-2$\sqrt{5}$) | D. | (-2$\sqrt{5}$,-$\sqrt{5}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $\frac{2015}{2016}$ | B. | $\frac{4032}{2017}$ | C. | $\frac{4030}{2016}$ | D. | $\frac{2016}{2017}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
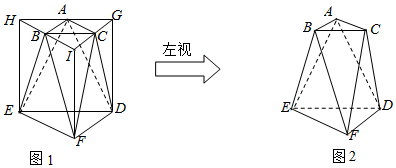 如图,把侧棱与底面垂直,且底面边长和侧棱长都等于的三棱柱截去三个角(如图1所示,A,B,C分别是△GHI三边的中点)后得到的几何体如图2所示,则该几何体按图中所示方向的左视图(侧视图)为( )
如图,把侧棱与底面垂直,且底面边长和侧棱长都等于的三棱柱截去三个角(如图1所示,A,B,C分别是△GHI三边的中点)后得到的几何体如图2所示,则该几何体按图中所示方向的左视图(侧视图)为( )| A. |  | B. | 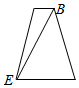 | C. | 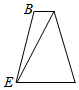 | D. | 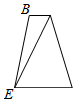 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 直角三角形 | B. | 锐角三角形 | C. | 钝角三角形 | D. | 等边三角形 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com