
【题目】2016年春节期间全国流行在微信群里发抢红包,现假设某人将688元发成手气红包50个,产生的手气红包频数分布表如下:
金额分组 |
|
|
|
|
|
|
频 数 | 3 | 9 | 17 | 11 | 8 | 2 |
(1)求产生的手气红包的金额不小于9元的频率;
(2)估计手气红包金额的平均数(同一组中的数据用该组区间的中点值作代表);
(3)在这50个红包组成的样本中,将频率视为概率.
①若红包金额在区间![]() 内为最佳运气手,求抢得红包的某人恰好是最佳运气手的概率;
内为最佳运气手,求抢得红包的某人恰好是最佳运气手的概率;
②随机抽取手气红包金额在![]() 内的两名幸运者,设其手气金额分别为
内的两名幸运者,设其手气金额分别为![]() ,
,![]() ,求事件“
,求事件“![]() ”的概率.
”的概率.
【答案】(1)![]() ;(2)平均数为:12.44;(3)①
;(2)平均数为:12.44;(3)①![]() ;②
;②![]()
【解析】
(1)由题意利用互斥事件概率加法公式能求出产生的手气红包的金额不小于9元的频率.
(2)先求出手气红包在![]() ,
,![]() 、
、![]() ,
,![]() 、
、![]() ,
,![]() 、
、![]() ,
,![]() 、
、![]() ,
,![]() 、
、![]() ,
,![]() 内的频率,由此能求了出手气红包金额的平均数.
内的频率,由此能求了出手气红包金额的平均数.
(3)①由题可知红包金额在区间![]() ,
,![]() 内有两人,由此能求出抢得红包的某人恰好是最佳运气手的概率.
内有两人,由此能求出抢得红包的某人恰好是最佳运气手的概率.
②由频率分布表可知,红包金额在![]() ,
,![]() 内有3人,在
内有3人,在![]() ,
,![]() 内有2人,由此能求出事件“
内有2人,由此能求出事件“![]() “的概率
“的概率![]() .
.
解:(1)由题意得产生的手气红包的金额不小于9元的频率:
![]() ,
,
![]() 产生的手气红包的金额不小于9元的频率为
产生的手气红包的金额不小于9元的频率为![]() .
.
(2)手气红包在![]() ,
,![]() 内的频率为
内的频率为![]() ,
,
手气红包在![]() ,
,![]() 内的频率为
内的频率为![]() ,
,
手气红包在![]() ,
,![]() 内的频率为
内的频率为![]() ,
,
手气红包在![]() ,
,![]() 内的频率为
内的频率为![]() ,
,
手气红包在![]() ,
,![]() 内的频率为
内的频率为![]() ,
,
手气红包在![]() ,
,![]() 内的频率为
内的频率为![]() ,
,
则手气红包金额的平均数为:
![]() .
.
(3)①由题可知红包金额在区间![]() ,
,![]() 内有两人,
内有两人,
![]() 抢得红包的某人恰好是最佳运气手的概率
抢得红包的某人恰好是最佳运气手的概率![]() .
.
②由频率分布表可知,红包金额在![]() ,
,![]() 内有3人,
内有3人,
设红包金额分别为![]() ,
,![]() ,
,![]() ,在
,在![]() ,
,![]() 内有2人,
内有2人,
设红包金额分别为![]() ,
,![]() ,
,
若![]() ,
,![]() 均在
均在![]() ,
,![]() 内,有3种情况:
内,有3种情况:![]() ,
,![]() ,
,![]() ,
,
若![]() ,
,![]() 均在
均在![]() ,
,![]() 内只有一种情况:
内只有一种情况:![]() ,
,
若![]() ,
,![]() 分别在
分别在![]() ,
,![]() 和
和![]() ,
,![]() 内,有6种情况,
内,有6种情况,
即![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() 基本事件总数
基本事件总数![]() ,
,
而事件“![]() “所包含的基本事件有6种,
“所包含的基本事件有6种,
![]() .
.


科目:高中数学 来源: 题型:
【题目】定义域均为D的三个函数![]() ,
,![]() ,
,![]() 满足条件:对任意
满足条件:对任意![]() ,点
,点![]() 与点
与点![]() 都关于点
都关于点![]() 对称,则称
对称,则称![]() 是
是![]() 关于
关于![]() 的“对称函数”.已知函数
的“对称函数”.已知函数![]() ,
,![]() ,
,![]() 是
是![]() 关于
关于![]() 的“对称函数“,记
的“对称函数“,记![]() 的定义域为D,若对任意
的定义域为D,若对任意![]() ,都存在
,都存在![]() ,使得
,使得![]() 成立,则实数a的取值范围是( )
成立,则实数a的取值范围是( )
A..![]() B..
B..![]() C..
C..![]() D..
D..![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】受新冠肺炎疫情影响,某学校按上级文件指示,要求错峰放学,错峰有序吃饭.高三年级一层楼六个班排队,甲班必须排在前三位,且丙班、丁班必须排在一起,则这六个班排队吃饭的不同安排方案共有( )
A.240种B.120种C.188种D.156种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() ,四点
,四点![]() ,
,![]() ,
,![]() ,
,![]() 中恰有三个点在椭圆
中恰有三个点在椭圆![]() 上,左、右焦点分别为
上,左、右焦点分别为![]() 、
、![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过左焦点![]() 且不与坐标轴平行的直线
且不与坐标轴平行的直线![]() 交椭圆于
交椭圆于![]() 、
、![]() 两点,若线段
两点,若线段![]() 的垂直平分线交
的垂直平分线交![]() 轴于点
轴于点![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为抑制房价过快上涨和过度炒作,各地政府响应中央号召,因地制宜出台了系列房价调控政策.某市拟定出台“房产限购的年龄政策”.为了解人们对“房产限购年龄政策”的态度,在2060岁的人群中随机调查100人,调查数据的频率分布直方图和支持“房产限购”的人数与年龄的统计结果如图所示:
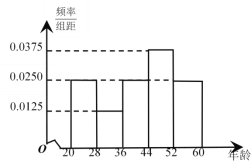
年龄 |
|
|
|
|
|
支持的人数 | 15 | 5 | 15 | 28 | 17 |
(1)由以上统计数据填![]() 列联表,并判断能否在犯错误的概率不超过0.05的前提下认为以44岁为分界点的不同人群对“房产限购年龄政策”的支持度有差异?
列联表,并判断能否在犯错误的概率不超过0.05的前提下认为以44岁为分界点的不同人群对“房产限购年龄政策”的支持度有差异?
44岁以下 | 44岁及44岁以上 | 总计 | |
支持 | |||
不支持 | |||
总计 |
(2)若以44岁为分界点,从不支持“房产限购”的人中按分层抽样的方法抽取8人参加政策听证会,现从这8人中随机抽2人.记抽到44岁以上的人数为![]() ,求随机变量
,求随机变量![]() 的分布列及数学期望.
的分布列及数学期望.
参考公式: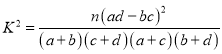 .
.
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(Ⅰ)不需证明,直接写出![]() 的奇偶性:
的奇偶性:
(Ⅱ)讨论![]() 的单调性,并证明
的单调性,并证明![]() 有且仅有两个零点:
有且仅有两个零点:
(Ⅲ)设![]() 是
是![]() 的一个零点,证明曲线
的一个零点,证明曲线![]() 在点
在点![]() 处的切线也是曲线
处的切线也是曲线![]() 的切线.
的切线.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 和圆
和圆![]() ,
,![]() 、
、![]() 为椭圆
为椭圆![]() 的左、右焦点,点
的左、右焦点,点![]() 在椭圆
在椭圆![]() 上,当直线
上,当直线![]() 与圆
与圆![]() 相切时,
相切时,![]() .
.
(I)求![]() 的方程;
的方程;
(Ⅱ)直线![]() 与椭圆
与椭圆![]() 和圆
和圆![]() 都相切,切点分别为
都相切,切点分别为![]() 、
、![]() ,求
,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com