
【题目】在棱长为2的正方体ABCD﹣A1B1C1D1中,点E是棱AA1的中点,则异面直线DE与BC所成的角的余弦值是 .
科目:高中数学 来源: 题型:
【题目】等轴双曲线C的中心在原点,焦点在x轴上,双曲线C与抛物线y2=16x的准线交于A,B两点,|AB|=4 ![]() ,则双曲线C的实轴长为( )
,则双曲线C的实轴长为( )
A.![]()
B.2 ![]()
C.4
D.4 ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足a1=2,且anan+1+an+1﹣2an=0(n∈N+).
(1)求a2、a3、a4的值;
(2)猜想数列{an}的通项公式,并用数学归纳法加以证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() +lnx在(1,+∞)上是增函数,且a>0.
+lnx在(1,+∞)上是增函数,且a>0.
(1)求a的取值范围;
(2)求函数g(x)=ln(1+x)﹣x在[0,+∞)上的最大值;
(3)设a>1,b>0,求证: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C:(x﹣1)2+(y﹣2)2=25,直线l:(2m+1)x+(m+1)y﹣7m﹣4=0.
(1)求证:直线l恒过定点;
(2)求直线l被圆C截得的弦长最长与最短的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知P是圆x2+y2=36的圆心,R是椭圆 ![]() 上的一动点,且满足
上的一动点,且满足 ![]() .
.
(1)求动点Q的轨迹方程
(2)若直线y=x+1与曲线Q相交于A、B两点,求弦AB的长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(用空间向量坐标表示解答)已知正三棱柱ABC﹣A1B1C1的各棱长都是4,E是BC的中点,F在CC1上,且CF=1. 
(1)求证:EF⊥A1C;
(2)求二面角C﹣AF﹣E的平面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我校为进行“阳光运动一小时”活动,计划在一块直角三角形ABC的空地上修建一个占地面积为S(平方米)的矩形AMPN健身场地.如图,点M在AC上,点N在AB上,且P点在斜边BC上.已知∠ACB=60°,|AC|=30米,|AM|=x米,x∈[10,20].设矩形AMPN健身场地每平方米的造价为 ![]() 元,再把矩形AMPN以外(阴影部分)铺上草坪,每平方米的造价为
元,再把矩形AMPN以外(阴影部分)铺上草坪,每平方米的造价为 ![]() 元(k为正常数).
元(k为正常数).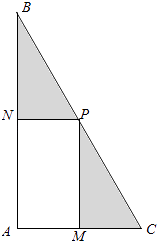
(1)试用x表示S,并求S的取值范围;
(2)求总造价T关于面积S的函数T=f(S);
(3)如何选取|AM|,使总造价T最低(不要求求出最低造价).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com