
设函数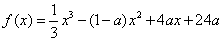 ,其中常数a>1
,其中常数a>1
(Ⅰ)讨论f(x)的单调性;
(Ⅱ)若当x≥0时,f(x)>0恒成立,求a的取值范围。
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:高中数学 来源: 题型:
一位幼儿园老师给班上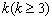 个小朋友分糖果.她发现糖果盒中原有糖果数为
个小朋友分糖果.她发现糖果盒中原有糖果数为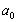 ,就先从别处抓2块糖加入盒中,然后把盒内糖果的
,就先从别处抓2块糖加入盒中,然后把盒内糖果的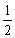 分给第一个小朋友;再从别处抓2块糖加入盒中,然后把盒内糖果的
分给第一个小朋友;再从别处抓2块糖加入盒中,然后把盒内糖果的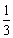 分给第二个小朋友;,以后她总是在分给一个小朋友后,就从别处抓2块糖放入盒中,然后把盒内糖果的
分给第二个小朋友;,以后她总是在分给一个小朋友后,就从别处抓2块糖放入盒中,然后把盒内糖果的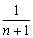 分给第
分给第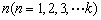 个小朋友.如果设分给第
个小朋友.如果设分给第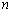 个小朋友后(未加入2块糖果前)盒内剩下的糖果数为
个小朋友后(未加入2块糖果前)盒内剩下的糖果数为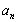 .
.
(1) 当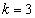 ,
,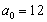 时,分别求
时,分别求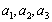 ;
;
(2) 请用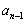 表示
表示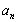 ;令
;令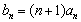 ,求数列
,求数列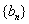 的通项公式;
的通项公式;
(3)是否存在正整数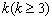 和非负整数
和非负整数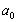 ,使得数列
,使得数列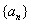
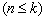 成等差数列,如果存在,请求出所有的
成等差数列,如果存在,请求出所有的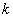 和
和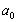 ,如果不存在,请说明理由.
,如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
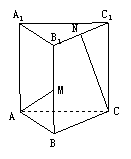 如图,在正三棱柱ABC-A1B1C1中,AB=AA1=2,M、N分别是BB1和B1C1的中点,则直线AM与CN所成角的余弦值等于( )
如图,在正三棱柱ABC-A1B1C1中,AB=AA1=2,M、N分别是BB1和B1C1的中点,则直线AM与CN所成角的余弦值等于( )
A.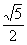 B.
B.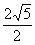 C.
C.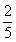 D.
D.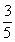
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com