
【题目】已知函数![]() ,
,![]() ,则
,则![]() 的零点个数为( )
的零点个数为( )
A. 6B. 7C. 8D. 9
 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案科目:高中数学 来源: 题型:
【题目】为弘扬中华民族传统文化,某中学学生会对本校高一年级1000名学生课余时间参加传统文化活动的情况,随机抽取50名学生进行调查,将数据分组整理后,列表如下:
参加场数 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
参加人数占调查人数的百分比 | 8% | 10% | 20% | 26% | 18% | 12% | 4% | 2% |
估计该校高一学生参加传统文化活动情况正确的是().
A. 参加活动次数是3场的学生约为360人B. 参加活动次数是2场或4场的学生约为480人
C. 参加活动次数不高于2场的学生约为280人D. 参加活动次数不低于4场的学生约为360人
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区随着经济的发展,居民收入逐年增长,银行储蓄连年增长,下表是该地区某银行连续五年的储蓄存款(年底结算):
年份 |
|
|
|
|
|
储蓄存款 |
|
|
|
|
|
为方便研究,工作人员对上表的数据做了如下处理:![]() ,
,![]() 得到下表:
得到下表:
|
|
|
|
|
|
|
|
|
|
|
|
(1)用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)通过(1)中的方程,求出![]() 关于
关于![]() 的线性回归方程,并用所求回归方程预测
的线性回归方程,并用所求回归方程预测![]() 年底,该地储蓄存款额可达多少?
年底,该地储蓄存款额可达多少?
(附:参考公式![]() ,其中
,其中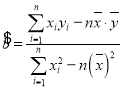 ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若定义在R上的函数f(x)满足f(x)+f′(x)>1,f(0)=4,则不等式f(x)>![]() +1(e为自然对数的底数)的解集为( )
+1(e为自然对数的底数)的解集为( )
A.(0,+∞)B.(-∞,0)∪(3,+∞)
C.(-∞,0)∪(0,+∞)D.(3,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知点E是圆心为O1半径为2的半圆弧上从点B数起的第一个三等分点,点F是圆心为O2半径为1的半圆弧的中点,AB、CD分别是两个半圆的直径,O1O2=2,直线O1O2与两个半圆所在的平面均垂直,直线AB、DC共面.
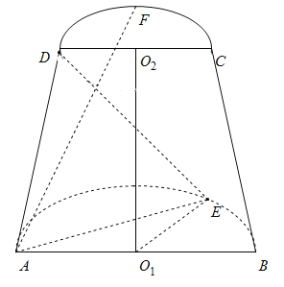
(1)求三棱锥D﹣ABE的体积;
(2)求直线DE与平面ABE所成的角的正切值;
(3)求直线AF与BE所成角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知,椭圆C过点![]() ,两个焦点为
,两个焦点为![]() ,
,![]() ,E,F是椭圆C上的两个动点,如果直线AE的斜率与AF的斜率互为相反数,直线EF的斜率为
,E,F是椭圆C上的两个动点,如果直线AE的斜率与AF的斜率互为相反数,直线EF的斜率为![]() ,直线l与椭圆C相切于点A,斜率为
,直线l与椭圆C相切于点A,斜率为![]() .
.
![]() 求椭圆C的方程;
求椭圆C的方程;
![]() 求
求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com