
����Ŀ��ijѧУ���б�ҵ��������![]() ��,Ů��
��,Ů��![]() ��,ѧУΪ�˶Ը���ѧ����ѧѧϰ������з���,�Ӹ����꼶�����Ա���зֲ����,��ȡ
��,ѧУΪ�˶Ը���ѧ����ѧѧϰ������з���,�Ӹ����꼶�����Ա���зֲ����,��ȡ![]() ��ѧ���ɼ�,ͳ���������±���ʾ:
��ѧ���ɼ�,ͳ���������±���ʾ:
������������ |
|
|
|
|
| �ܼ� |
Ƶ�� |
|
|
|
|
|
|
��1�����ɼ���![]() ����������
����������![]() ����,��ɼ�Ϊ����,����Ƹ�У��ҵ��ƽ���ɼ��ͼ���ѧ������;
����,��ɼ�Ϊ����,����Ƹ�У��ҵ��ƽ���ɼ��ͼ���ѧ������;
��2���������������,��60��Ů����ѧ�ɼ�����,�����������ѧ�ɼ����Ա��������,���ж��Ƿ���![]() �İ�����Ϊ������Уѧ������ѧ�ɼ����Ա��й���.
�İ�����Ϊ������Уѧ������ѧ�ɼ����Ա��й���.
Ů�� | ���� | �ܼ� | |
�������� |
| ||
���������� | |||
�ܼ� |
�ο���ʽ:![]()
|
|
|
|
|
|
|
|
���𰸡���1��ƽ���ɼ�101�֣���������1050�ˣ���2��û��90%�İ�����Ϊ����Уѧ������ѧ�ɼ����Ա��й���
��������
���������
��1����ͳ�����ݿ�֪��������ÿ��ɼ����е�ֵ�����ƽ���ɼ�������ȡ��200�˵�ƽ���ɼ�Ϊ![]() �֣��ɼ���90������90�������ϵ�����Ϊ70+50+20=140�ˣ�ռ200�˵ı���Ϊ
�֣��ɼ���90������90�������ϵ�����Ϊ70+50+20=140�ˣ�ռ200�˵ı���Ϊ![]() ����˿��Թ��Ƹ�У��ҵ��1500�˼�������ԼΪ
����˿��Թ��Ƹ�У��ҵ��1500�˼�������ԼΪ![]() �ˡ���2�������Ǵ�1500���а��ֲ������ȡ����������������Ϊ200�����Ը�200���У�Ů������ӦΪ
�ˡ���2�������Ǵ�1500���а��ֲ������ȡ����������������Ϊ200�����Ը�200���У�Ů������ӦΪ![]() �ˣ�������Ů������Ϊ60�����Բ�����Ů������Ϊ20���ָ��ݵ���1���ʣ��ɼ���90������90��������Ϊ��������200���м�������Ϊ140����ô����������������ӦΪ80�ˣ�������������ӦΪ40�ˣ�����2��2�������е����ݾ���֪�����Ը��ݸ����IJο���ʽ�����Լ���
�ˣ�������Ů������Ϊ60�����Բ�����Ů������Ϊ20���ָ��ݵ���1���ʣ��ɼ���90������90��������Ϊ��������200���м�������Ϊ140����ô����������������ӦΪ80�ˣ�������������ӦΪ40�ˣ�����2��2�������е����ݾ���֪�����Ը��ݸ����IJο���ʽ�����Լ���![]() ������û��90%�İ�����Ϊ����Уѧ������ѧ�ɼ����Ա��й��������⿼�����ͳ��֪ʶ�������Լ�����㼰�жϣ����ڻ����⡣
������û��90%�İ�����Ϊ����Уѧ������ѧ�ɼ����Ա��й��������⿼�����ͳ��֪ʶ�������Լ�����㼰�жϣ����ڻ����⡣
�����������1���⣺����ѧ����ѧƽ���ɼ�Ϊ![]()
���Ƹ���ѧ����ѧƽ���ɼ�ԼΪ101��
����ѧ������Ϊ![]()
��2���⣺
Ů�� | ���� | �ܼ� | |
�������� | 60 | 80 | 140 |
���������� | 20 | 40 | 60 |
�ܼ� | 80 | 120 | 200 |
![]() �Ĺ۲�ֵ
�Ĺ۲�ֵ![]()
����û��90%�İ�����Ϊ����Уѧ������ѧ�ɼ����Ա��й���.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������![]()
![]() ��
��![]() ���㣺
���㣺
��1��![]() ��
��
��2��������![]() �������ֵ����Сֵ��
�������ֵ����Сֵ��
��3��������![]() ������Сֵ�����ֵ��
������Сֵ�����ֵ��
��4������![]() ��
��
��1����![]() �Ľ���ʽ��
�Ľ���ʽ��
��2����![]() ����
����![]() ֵ;
ֵ;
��3������ʽ![]() �Ľ⼯��Ϊ�ռ�����ʵ��
�Ľ⼯��Ϊ�ռ�����ʵ��![]() �ķ�Χ.
�ķ�Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����![]() �ǹ���Ϊ�������ĵȱ����У�
�ǹ���Ϊ�������ĵȱ����У�![]() �ǵȲ����У���
�ǵȲ����У���![]() ��
��![]() ��
��![]() .
.
��1��������![]() ��
��![]() ��ͨ�ʽ��
��ͨ�ʽ��
��2���� ����
����![]() ��ǰ
��ǰ![]() ���Ϊ
���Ϊ![]() .
.
��������С��������![]() ��ʹ����
��ʹ����![]() ʱ������
ʱ������![]() ������
������
���Ƿ����������![]()
![]() ��ʹ��
��ʹ��![]() �����������ڣ��������������������
�����������ڣ��������������������![]() ���������ڣ���˵������.
���������ڣ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Բ![]() ��һ������Ϊ
��һ������Ϊ![]() �����Ҷ���ֱ�Ϊ
�����Ҷ���ֱ�Ϊ![]() ��������
��������![]() ��ֱ��
��ֱ��![]() ����Բ
����Բ![]() ����
����![]() ����.
����.
��1������Բ���̣�
��2����![]() ��
��![]() ������ֱ�Ϊ
������ֱ�Ϊ![]() ��
��![]() ����
����![]() �����ֵ.
�����ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ѡ��4��1������֤��ѡ��
��ͼ���ı���![]() �ڽ�����
�ڽ�����![]() ������
������![]() ����
����![]() ������
������![]() ��
��![]() ���ӳ�����
���ӳ�����![]() ����֪
����֪![]() .
.

֤����
��1��![]() ��
��
��2��![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��
����ͼ��![]() �ǵ���ֱ�������Σ�
�ǵ���ֱ�������Σ�![]() ��
��![]() ��
��![]() �ֱ�Ϊ
�ֱ�Ϊ![]() ���е㣬��
���е㣬��![]() ��
��![]() ����ʹ�ö����
����ʹ�ö����![]() Ϊ
Ϊ![]() ��
��
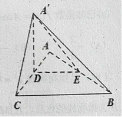
��1����֤��![]() ��
��
��2����ƽ��![]() ��ƽ��
��ƽ��![]() �нǵ�����ֵ��
�нǵ�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳�Ϊ�����˿������Ƴ�һ���Żݻ����������£����Ѷ�ÿ��100Ԫ��ת����ͼ��ʾ��ת��һ�Σ��������Ӧ���ķ�ȯ���ٶ�ָ��ȿ��ܵ�ͣ����һλ�ã� ��ָ��ͣ��A����ȯ60Ԫ��ͣ��B����ȯ30Ԫ��ͣ��C����ȯ�� ���磺����218Ԫ����ת��ת��2�Σ�����õķ�ȯ��������ν��֮�ͣ�

��1����ijλ�˿�����128Ԫ����ȯ������30Ԫ�ĸ��ʣ�
��2����ijλ�˿�ǡ������280Ԫ��������������˻������÷�ȯ�Ľ���Ϊ![]() ��Ԫ�������������
��Ԫ�������������![]() �ķֲ��к���ѧ������
�ķֲ��к���ѧ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Բ![]() ��
��![]() ��������Ϊ
��������Ϊ![]() �������ĸ�����Ϊ������ı��ε��������
�������ĸ�����Ϊ������ı��ε��������![]() .
.
��1������Բ![]() �ı����̣�
�ı����̣�
��2����ԭ����б�ʲ�Ϊ0��ֱ��![]() ����Բ
����Բ![]() ����
����![]() ���㣬
���㣬![]() ����Բ
����Բ![]() ���Ҷ��㣬ֱ��
���Ҷ��㣬ֱ��![]() �ֱ���
�ֱ���![]() �ύ�ڵ�
�ύ�ڵ�![]() ���ʣ���
���ʣ���![]() Ϊֱ����Բ�Ƿ���
Ϊֱ����Բ�Ƿ���![]() ���ϵĶ��㣿�����ڣ�������ö�������ꣻ�������ڣ���˵������.
���ϵĶ��㣿�����ڣ�������ö�������ꣻ�������ڣ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ��3x��4y+5=0����x��ԳƵ�ֱ�ߵķ����ǣ� ��
A.3x��4y+5=0
B.3x��4y��5=0
C.3x+4y��5=0
D.3x+4y+5=0
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com