
【题目】已知椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,以其四个顶点为顶点的四边形的面积等于
,以其四个顶点为顶点的四边形的面积等于![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)过原点且斜率不为0的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,
两点,![]() 是椭圆
是椭圆![]() 的右顶点,直线
的右顶点,直线![]() 分别与
分别与![]() 轴交于点
轴交于点![]() ,问:以
,问:以![]() 为直径的圆是否恒过
为直径的圆是否恒过![]() 轴上的定点?若存在,请求出该定点的坐标;若不存在,请说明理由.
轴上的定点?若存在,请求出该定点的坐标;若不存在,请说明理由.
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】为了解篮球爱好者小李的投篮命中率与打篮球时间的关系,下表记录了小李某月连续5天每天打篮球时间![]() (单位:小时)与当天投篮命中率
(单位:小时)与当天投篮命中率![]() 之间的关系:
之间的关系:
时间 | 1 | 2 | 3 | 4 | 5 |
命中率 | 0.4 | 0.5 | 0.6 | 0.6 | 0.4 |
(Ⅰ)请根据上表提供的数据,用最小二乘法求出投篮命中率![]() 与打篮球时间
与打篮球时间![]() (单位:小时)之间的回归直线方程
(单位:小时)之间的回归直线方程![]() ;
;
(Ⅱ)如果小李某天打了2.5小时篮球,预测小李当天的投篮命中率.
(参考:用最小二乘法求线性回归方程系数公式 ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校高中毕业班有男生![]() 人,女生
人,女生![]() 人,学校为了对高三学生数学学习情况进行分析,从高三年级按照性别进行分层抽样,抽取
人,学校为了对高三学生数学学习情况进行分析,从高三年级按照性别进行分层抽样,抽取![]() 名学生成绩,统计数据如下表所示:
名学生成绩,统计数据如下表所示:
分数段(分) |
|
|
|
|
| 总计 |
频数 |
|
|
|
|
|
|
(1)若成绩在![]() 分以上(含
分以上(含![]() 分),则成绩为及格,请估计该校毕业班平均成绩和及格学生人数;
分),则成绩为及格,请估计该校毕业班平均成绩和及格学生人数;
(2)如果样本数据中,有60名女生数学成绩及格,请完成如下数学成绩与性别的列联表,并判断是否有![]() 的把握认为:“该校学生的数学成绩与性别有关”.
的把握认为:“该校学生的数学成绩与性别有关”.
女生 | 男生 | 总计 | |
及格人数 |
| ||
不及格人数 | |||
总计 |
参考公式:![]()
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
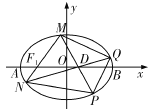
【题目】(本小题满分12分)如图,在平面直角坐标系![]() 中, 已知
中, 已知![]() 分别是椭圆
分别是椭圆![]() 的左、右焦点
的左、右焦点![]() 分别是椭圆
分别是椭圆![]() 的左、右顶点,
的左、右顶点,![]() 为线段
为线段![]() 的中点, 且
的中点, 且![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若![]() 为椭圆
为椭圆![]() 上的动点(异于点
上的动点(异于点![]() ),连接
),连接![]() 并延长交椭圆
并延长交椭圆![]() 于点
于点![]() ,连接
,连接![]() 、
、![]() 并分别延
并分别延
长交椭圆![]() 于点
于点![]() 连接
连接![]() ,设直线
,设直线![]() 、
、![]() 的斜率存在且分别为
的斜率存在且分别为![]() 、
、![]() ,试问是否存在常数
,试问是否存在常数![]() ,使
,使
得![]() 恒成立?若存在,求出
恒成立?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,
,![]() 、
、![]() 是椭圆的左、右焦点,过
是椭圆的左、右焦点,过![]() 作直线
作直线![]() 交椭圆于
交椭圆于![]() 、
、![]() 两点,若
两点,若![]() 的周长为8.
的周长为8.
(1)求椭圆方程;
(2)若直线![]() 的斜率不为0,且它的中垂线与
的斜率不为0,且它的中垂线与![]() 轴交于
轴交于![]() ,求
,求![]() 的纵坐标的范围;
的纵坐标的范围;
(3)是否在![]() 轴上存在点
轴上存在点![]() ,使得
,使得![]() 轴平分
轴平分![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知极坐标的极点在平面直角坐标系的原点![]() 处,极轴与
处,极轴与![]() 轴的正半轴重合,且长度单位相同。
轴的正半轴重合,且长度单位相同。
直线![]() 的极坐标方程为:
的极坐标方程为: ,点
,点![]() ,参数
,参数![]() 。
。
(1)求点![]() 轨迹的直角坐标方程;
轨迹的直角坐标方程;
(2)求点![]() 到直线
到直线![]() 距离的最大值。
距离的最大值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙、丙、丁四位歌手参加比赛,只有其中一位获奖.有人走访了四位歌手,甲说:“是乙或丙获奖.”乙说:“甲、丙都未获奖.”丙说:“我获奖了.”丁说:“是乙获奖.”四位歌手的话只有两句是对的,则获奖的歌手是( )
A.甲
B.乙
C.丙
D.丁
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com