
【题目】如图,在以![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的五面体中,平面
为顶点的五面体中,平面![]() 平面
平面![]() ,
,![]() 是边长为
是边长为![]() 的正三角形,直线
的正三角形,直线![]() 与平面
与平面![]() 所成角为
所成角为![]() .
.
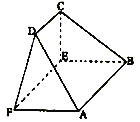
(I)求证:![]() ;
;
(Ⅱ)若![]() ,四边形
,四边形![]() 为平行四边形,求平面
为平行四边形,求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
【答案】(I)证明见解析;(Ⅱ)![]() .
.
【解析】
(I)过![]() 作
作![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,先证明
,先证明![]() 平面
平面![]() ,再由
,再由![]() 平面
平面![]() ,得出
,得出![]() 。
。
(Ⅱ)以![]() ,
,![]() ,
,![]() 为轴,建立空间直角坐标系,分别求出平面
为轴,建立空间直角坐标系,分别求出平面![]() 、平面
、平面![]() 的法向量
的法向量![]() 、
、![]() ,再由
,再由![]()
![]() 得出平面
得出平面![]() 与平面
与平面![]() 所成锐二面角的余弦值。
所成锐二面角的余弦值。
证明:(I)过![]() 作
作![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,
,
由平面![]() 平面
平面![]() ,得
,得![]() 平面
平面![]() ,∴
,∴![]() ,
,
又![]() ,
,![]() ,∴
,∴![]() ,∴
,∴![]() .
.
由直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,易得
,易得![]() ,
,
由![]() ,得
,得![]() ,又
,又![]() ,得
,得![]() .
.
由![]() ,
,![]() ,
,![]() ,
,![]() 平面
平面![]() ,得
,得![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,∴
,∴![]() .
.

(Ⅱ)由(I),![]() ,
,![]() ,
,![]() 两两垂直,以
两两垂直,以![]() 为坐标原点,建立如图所示空间直角坐标系
为坐标原点,建立如图所示空间直角坐标系![]() ,由题意
,由题意![]() ,
,![]() ,∴
,∴![]() ,
,
四边形![]() 为平行四边形,∴
为平行四边形,∴![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,∴
,∴![]() ,
,![]() .
.
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,由
,由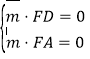 ,得
,得![]() ,取
,取![]() ,得
,得![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,
, ,
,![]() ,取
,取![]() ,
,![]() ,
,
![]() ,∴所求锐二面角的余弦值为
,∴所求锐二面角的余弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知△ABC的三边BC,CA,AB的中点分别是D(5,3),E(4,2),F(1,1).
(1)求△ABC的边AB所在直线的方程及点A的坐标;
(2)求△ABC的外接圆的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大型超市公司计划在![]() 市新城区开设分店,为确定在新城区开设分店的个数,该公司对该市已开设分店的其他区的数据统计后得到下列信息(其中
市新城区开设分店,为确定在新城区开设分店的个数,该公司对该市已开设分店的其他区的数据统计后得到下列信息(其中![]() 表示在该区开设分店的个数,
表示在该区开设分店的个数,![]() 表示这
表示这![]() 个分店的年收入之和):
个分店的年收入之和):
分店个数 | 2 | 3 | 4 | 5 | 6 |
年收入 | 250 | 300 | 400 | 450 | 600 |
(Ⅰ)该公司经过初步判断,可用线性回归模型拟合![]() 与
与![]() 的关系,求
的关系,求![]() 关于
关于![]() 的回归方程;
的回归方程;
(Ⅱ)假设该公司每年在新城区获得的总利润![]() (单位:万元)与
(单位:万元)与![]() ,
,![]() 之间的关系为
之间的关系为![]() ,请根据(Ⅰ)中的线性回归方程,估算该公司在新城区开设多少个分店时,才能使新城区每年每个分店的平均利润最大.
,请根据(Ⅰ)中的线性回归方程,估算该公司在新城区开设多少个分店时,才能使新城区每年每个分店的平均利润最大.
参考公式:回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为: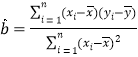
 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对以下命题:
①随机事件的概率与频率一样,与试验重复的次数有关;
②抛掷两枚均匀硬币一次,出现一正一反的概率是![]() ;
;
③若一种彩票买一张中奖的概率是![]() ,则买这种彩票一千张就会中奖;
,则买这种彩票一千张就会中奖;
④“姚明投篮一次,求投中的概率”属于古典概型概率问题.
其中正确的个数是( )
A.0B.1C.2D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,已知点![]() 是抛物线
是抛物线![]() 上一定点,直线
上一定点,直线![]() 的倾斜角互补,且与抛物线另交于
的倾斜角互补,且与抛物线另交于![]() ,
,![]() 两个不同的点.
两个不同的点.

(1)求点![]() 到其准线的距离;
到其准线的距离;
(2)求证:直线![]() 的斜率为定值.
的斜率为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 与
与![]() 轴负半轴相交于点
轴负半轴相交于点![]() ,与
,与![]() 轴正半轴相交于点
轴正半轴相交于点![]() .
.
(1)若过点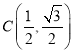 的直线
的直线![]() 被圆
被圆![]() 截得的弦长为
截得的弦长为![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)若在以![]() 为圆心,半径为
为圆心,半径为![]() 的圆上存在点
的圆上存在点![]() ,使得
,使得![]() (
(![]() 为坐标原点),求
为坐标原点),求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为响应低碳绿色出行,某市推出“新能源分时租赁汽车”,其中一款新能源分时租赁汽车,每次租车收费得标准由以下两部分组成:(1)根据行驶里程数按1元/公里计费;(2)当租车时间不超过40分钟时,按0.12元/分钟计费;当租车时间超过40分钟时,超出的部分按0.20元/分钟计费;(3)租车时间不足1分钟,按1分钟计算.已知张先生从家里到公司的距离为15公里,每天租用该款汽车上下班各一次,且每次租车时间t20,60(单位:分钟).由于堵车,红绿灯等因素,每次路上租车时间t是一个随即变量.现统计了他50次路上租车时间,整理后得到下表:
租车时间t(分钟) | [20,30] | (30,40] | (40,50] | (50,60] |
频数 | 2 | 18 | 20 | 10 |
将上述租车时间的频率视为概率.
(1)写出张先生一次租车费用y(元)与租车时间t(分钟)的函数关系式;
(2)公司规定,员工上下班可以免费乘坐公司接送车,若不乘坐公司接送车的每月(按22天计算)给800元车补.从经济收入的角度分析,张先生上下班应该选择公司接送车,还是租用该款新能源汽车?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校组织的一次教师招聘共分笔试和面试两个环节,笔试环节共有20名大学毕业生参加,其中男、女生的比例恰好为![]() ,其成绩的茎叶图如图所示.假设成绩在90分以上的考生可以进入面试环节.
,其成绩的茎叶图如图所示.假设成绩在90分以上的考生可以进入面试环节.
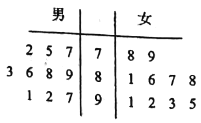
(1)试比较男、女两组成绩平均分的大小,并求出女生组的方差;
(2)从男、女两组可以进入面试环节的考生中分别任取1人,求两人分差不小于3分的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com