练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

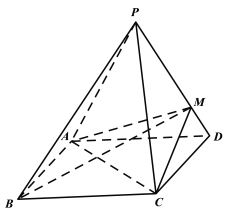
    【题目】如图，四棱锥P－ABCD的底面是矩形，侧面PAD为等边三角形，AB＝，AD＝， PB＝.

    （1）求证：平面PAD⊥平面ABCD；

    （2）M是棱PD上一点，三棱锥M－ABC的体积为1.记三棱锥P－MAC的体积为，三棱锥M－ACD的体积为，求.

    【答案】（1）详见解析；（2）.

    【解析】

    （1）由勾股定理可得，又，可得平面，可得平面平面；

    （2）由三棱锥与三棱锥等底同高，可得，又由正三角形的高也就是三棱锥的高，计算出三棱锥的体积，从而得出，再得出的值.

    （1）由已知，得，于是，故，

    因为四边形ABCD是矩形，所以，又，所以平面，因为平面，

    所以：平面平面.

    （2）依题意，得三棱锥与三棱锥等底同高，所以，

    又正三角形中，，所以正三角形的高为,

    由（1）得正三角形的高也就是三棱锥的高，

    所以，

    所以，故.

    故得解.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】某租赁公司拥有汽车100辆.当每辆车的月租金为3000元时，可全部租出.当每辆车的月租金每增加元时，未租出的车将会增加一辆.租出的车每辆每月需要维护费元，未租出的车每辆每月需要维护费元.

    （1）当每辆车的月租金定为元时，能租出多少辆车？

    （2）当每辆车的月租金定为多少元时，租赁公司的月收益最大？最大月收益是多少？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】世界那么大，我想去看看，处在具有时尚文化代表的大学生们旅游动机强烈，旅游可支配收入日益增多，可见大学生旅游是一个巨大的市场.为了解大学生每年旅游消费支出（单位：百元）的情况，相关部门随机抽取了某大学的名学生进行问卷调查，并把所得数据列成如下所示的频数分布表：

    组别

    频数

    （Ⅰ）求所得样本的中位数（精确到百元）；

    （Ⅱ）根据样本数据，可近似地认为学生的旅游费用支出服从正态分布，若该所大学共有学生人，试估计有多少位同学旅游费用支出在元以上；

    （Ⅲ）已知样本数据中旅游费用支出在范围内的名学生中有名女生， 名男生，现想选其中名学生回访，记选出的男生人数为，求的分布列与数学期望.

    附：若，则，

    ， .

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数

    (1)求f(x)的最小正周期及单调减区间；

    (2)若α∈(0，π)，且f＝，求tan的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在三棱锥中，，平面和平面所成角为，则三棱锥外接球的体积为（ ）

    A. B. C. D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知定义域为的函数是奇函数.

    (1) 求实数的值；

    (2) 判断并用定义证明该函数在定义域上的单调性；

    (3) 若方程在内有解，求实数的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知为圆上一动点，圆心关于轴的对称点为，点分别是线段上的点，且.

    （1）求点的轨迹方程；

    （2）直线与点的轨迹只有一个公共点，且点在第二象限，过坐标原点且与垂直的直线与圆相交于两点，求面积的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】椭圆的离心率是，过点的动直线与椭圆相交于两点，当直线与轴平行时，直线被椭圆截得的线段长为.

    （Ⅰ）求椭圆的方程；

    （Ⅱ）在轴上是否存在异于点的定点，使得直线变化时，总有？若存在，求出点的坐标；若不存在，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】函数f（x）＝Asin（ωx）+1（A＞0，ω＞0）的最大值为3，其图象相邻两条对称轴之间的距离为．

    （1）求函数f（x）的解析式；

    （2）求函数y＝f（x）的单调增区间；

    （3）设α∈（0，），则f（）＝2，求α的值．

    查看答案和解析>>

    同步练习册答案