
| A. | (1,+∞) | B. | [1,+∞) | C. | (-∞,1) | D. | (-∞,1] |
分析 g(x)=f(x)-x-a只有一个零点可化为函数f(x)与函数y=x+a有一个交点,作函数f(x)=$\left\{\begin{array}{l}{{2}^{-x}-1,x≤0}\\{f(x-1),x>0}\end{array}\right.$与函数y=x+a的图象,结合图象可直接得到答案.
解答 解:∵g(x)=f(x)-x-a只有一个零点,
∴函数y=f(x)与函数y=x+a有一个交点,
作函数f(x)=$\left\{\begin{array}{l}{{2}^{-x}-1,x≤0}\\{f(x-1),x>0}\end{array}\right.$与函数y=x+a的图象如下,
结合图象可知,
a≥1;
故选:B.
点评 本题考查了函数的零点与函数图象的交点的关系应用及数形结合的思想应用,属于中档题.


 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | (-∞,2] | B. | (1,2) | C. | (1,+∞) | D. | (2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{3}{8}$ | C. | $\frac{1}{2}$ | D. | $\frac{5}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
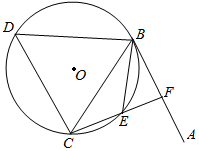 如图,直线AB为⊙O的切线,切点为B,点C、D在圆上,DB=DC,作BE⊥BD交圆于点E
如图,直线AB为⊙O的切线,切点为B,点C、D在圆上,DB=DC,作BE⊥BD交圆于点E查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若Χ2的观测值为6.64,而P(Χ2≥6.64)=0.010,故我们有99%的把握认为吸烟与患肺病有关系,那么在100个吸烟的人中必有99人患有肺病 | |
| B. | 从独立性检验可知有99%的把握认为吸烟与患肺病有关系时,我们说某人吸烟,那么他有99%的可能患有肺病 | |
| C. | 若从统计量中求出有95%的把握认为吸烟与患肺病有关系,是指有5%的可能性使得推判出现错误 | |
| D. | 以上三种说法都不正确 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
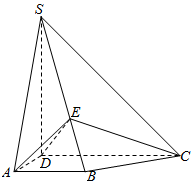 如图,四棱锥S-ABCD中,SD⊥底面ABCD,AB∥DC,AD⊥DC,AB=AD=1,DC=SD=2,E为棱SB上的一点,平面EDC⊥平面SBC.
如图,四棱锥S-ABCD中,SD⊥底面ABCD,AB∥DC,AD⊥DC,AB=AD=1,DC=SD=2,E为棱SB上的一点,平面EDC⊥平面SBC.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com