
 四面体ABCD及其三视图如图所示,点E、F、G、H分别是棱AB、BD、DC、CA的中点.
四面体ABCD及其三视图如图所示,点E、F、G、H分别是棱AB、BD、DC、CA的中点.分析 (1)证明:四边形EFGH是平行四边形,AD⊥平面BDC,即可证明四边形EFGH是矩形;
(2)S四面体ABCD=S△ABD+S△ACD+S△BCD+S△ABC,即可求四面体ABCD的表面积.
(3)以D为坐标原点建立空间直角坐标系,利用向量的方法求直线AB与平面EFGH夹角θ的正弦值.
解答  (1)证明:由该四面体的三视图可知,
(1)证明:由该四面体的三视图可知,
BD⊥DC,BD⊥AD,AD⊥DC,BD=DC=2,AD=1.
由题设可知,BC∥FG,BC∥EH,∴FG∥EH.
EF∥AD,HG∥AD,∴EF∥HG.
∴四边形EFGH是平行四边形.
又∵AD⊥DC,AD⊥BD,∴AD⊥平面BDC,
∴AD⊥BC,∴EF⊥FG,∴四边形EFGH是矩形.
(2)解:由三视图可知,BD=DC=2,AD=1,则有AB=AC=$\sqrt{5}$,BC=2$\sqrt{2}$
∴S△ABD=S△ACD=$\frac{1}{2}×2×1$=1,S△BCD=$\frac{1}{2}×2×2$=2,S△ABC=$\frac{1}{2}×2\sqrt{2}×\sqrt{3}$=$\sqrt{6}$
∴S四面体ABCD=S△ABD+S△ACD+S△BCD+S△ABC=4+$\sqrt{6}$
(3)解:如图,以D为坐标原点建立空间直角坐标系,
则D(0,0,0),A(0,0,1),B(2,0,0),C(0,2,0),
∵E是AB的中点,∴F,G分别为BD,DC的中点,
得E(1,0,$\frac{1}{2}$),F(1,0,0),G(0,1,0).
∴$\overrightarrow{FE}$=(0,0,$\frac{1}{2}$),$\overrightarrow{FG}$=(-1,1,0),$\overrightarrow{BA}$=(-2,0,1).
设平面EFGH的法向量$\overrightarrow{n}$=(x,y,z),
得$\left\{\begin{array}{l}\frac{1}{2}z=0\\-x+y=0\end{array}$取$\overrightarrow{n}$=(1,1,0),
∴sin θ=|cos<$\overrightarrow{BA}$,$\overrightarrow{n}$>|=$\frac{2}{\sqrt{5}×\sqrt{2}}$=$\frac{\sqrt{10}}{5}$.
点评 本题考查线面垂直的判定与性质,考查面积的计算,考查向量方法的运用,正确求出平面的法向量是关键.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
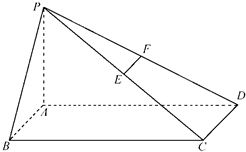 如图,四棱锥P-ABCD的底面ABCD是矩形,PA⊥底面ABCD,E、F分别是PC、PD的中点,PA=$\sqrt{3}$AD.
如图,四棱锥P-ABCD的底面ABCD是矩形,PA⊥底面ABCD,E、F分别是PC、PD的中点,PA=$\sqrt{3}$AD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年龄(岁) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75) |
| 频数 | 5 | 10 | 15 | 10 | 5 | 5 |
| 赞成人数 | 5 | 10 | 12 | 7 | 2 | 1 |
| 年龄不低于45岁的人 | 年龄低于45岁的人 | 合计 | |
| 赞成 | |||
| 不赞成 | |||
| 合计 |
| P(K2≥k0) | 0.050 | 0.010 | 0.001 |
| k0 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 汉诺塔的游戏规则如下:如图有A,B,C三根套杆,在A上有n个大小不等的盘子,中间有孔可以套在杆子上面,大盘在下,小盘在下,现在要将A杆上面的所有盘子合部移动到C杆上面,每次只能移动一个盘子,且每根杆子上面的所有盘子大盘不能压在小盘上面;n个盘子全部移动完成后,所需的最少移动次数记为vn,例如v1=1,v2=3;请你耐心寻找规律,计算v5=( )
汉诺塔的游戏规则如下:如图有A,B,C三根套杆,在A上有n个大小不等的盘子,中间有孔可以套在杆子上面,大盘在下,小盘在下,现在要将A杆上面的所有盘子合部移动到C杆上面,每次只能移动一个盘子,且每根杆子上面的所有盘子大盘不能压在小盘上面;n个盘子全部移动完成后,所需的最少移动次数记为vn,例如v1=1,v2=3;请你耐心寻找规律,计算v5=( )| A. | 31 | B. | 15 | C. | 11 | D. | 9 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com