
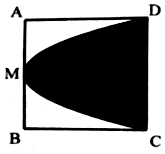
 如图,在边长为2的正方形ABCD中,M是AB的中点,则过C,M,D三点的抛物线与CD围成阴影部分的面积是( )
如图,在边长为2的正方形ABCD中,M是AB的中点,则过C,M,D三点的抛物线与CD围成阴影部分的面积是( )| A. | $\frac{2}{3}$ | B. | $\frac{4}{3}$ | C. | $\frac{5}{2}$ | D. | $\frac{8}{3}$ |
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
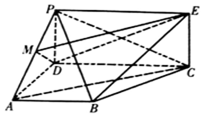 如图,四边形PDCE为矩形,四边形ABCD为梯形,平面PDCE⊥平面ABCD,∠BAD=∠ADC=90°,AB=AD=$\frac{1}{2}$CD=1.
如图,四边形PDCE为矩形,四边形ABCD为梯形,平面PDCE⊥平面ABCD,∠BAD=∠ADC=90°,AB=AD=$\frac{1}{2}$CD=1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 16 | B. | $16\sqrt{3}$ | C. | 32 | D. | $32\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
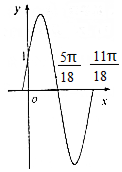 函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<$\frac{π}{2}$)的部分图象如图所示,则f($\frac{5π}{9}$)的值是( )
函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<$\frac{π}{2}$)的部分图象如图所示,则f($\frac{5π}{9}$)的值是( )| A. | 1 | B. | -1 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
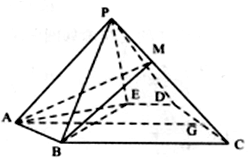 如图,在五棱锥P-ABCDE中,△ABE是等边三角形,四边形BCDE是直角梯形且∠DEB=∠CBE=90°,G是CD的中点,点P在底面的射影落在线段AG上.
如图,在五棱锥P-ABCDE中,△ABE是等边三角形,四边形BCDE是直角梯形且∠DEB=∠CBE=90°,G是CD的中点,点P在底面的射影落在线段AG上.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
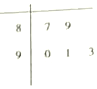 2017年2月20日,摩拜单车在济南推出“做文明骑士,周一摩拜单车免费骑”活动,为了解单车使用情况,记者随机抽取了五个投放区域,统计了半小时内被骑走的单车数量,绘制了如图所示的茎叶图,则该组数据的方差为( )
2017年2月20日,摩拜单车在济南推出“做文明骑士,周一摩拜单车免费骑”活动,为了解单车使用情况,记者随机抽取了五个投放区域,统计了半小时内被骑走的单车数量,绘制了如图所示的茎叶图,则该组数据的方差为( )| A. | 9 | B. | 4 | C. | 3 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com