
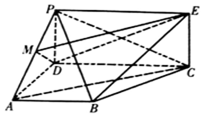
 如图,四边形PDCE为矩形,四边形ABCD为梯形,平面PDCE⊥平面ABCD,∠BAD=∠ADC=90°,AB=AD=$\frac{1}{2}$CD=1.
如图,四边形PDCE为矩形,四边形ABCD为梯形,平面PDCE⊥平面ABCD,∠BAD=∠ADC=90°,AB=AD=$\frac{1}{2}$CD=1.分析 (Ⅰ)设PC交DE于点N,连结MN,推导出MN∥AC,由此能证明AC∥平面MDE.
(Ⅱ)推导出∠PBD为PB与平面ABCD所成角,从而PD=BD=$\sqrt{2}$,设D到平面PBC的距离为d,由S△BDC•PD=S△PBC•d,能求出点D到平面PBC的距离.
解答 证明:(Ⅰ)设PC交DE于点N,连结MN,
在△PAC中,∵M,N分别为PA,PC的中点,
∴MN∥AC,又AC?平面MDE,MN?平面MDE,
∴AC∥平面MDE.
解:(Ⅱ)∵平面PDCE⊥平面ABCD,四边形PDCE为矩形,
∴PD⊥平面ABCD,∴∠PBD为PB与平面ABCD所成角,
∵PB与平面ABCD所成角为45°,
∴PD=BD=$\sqrt{2}$,
设D到平面PBC的距离为d,
∴$\frac{1}{3}$S△BDC•PD=$\frac{1}{3}$S△PBC•d,
∵${S}_{△BDC}=1,{S}_{△PBC}=\sqrt{2}$,
∴d=1,
∴点D到平面PBC的距离为1.
点评 本题考查线面平行的证明,考查点到平面的距离的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.


科目:高中数学 来源: 题型:选择题
 如图,在△ABC中,AB=BC=$\sqrt{6}$,∠ABC=90°,点D为AC的中点,将△ABD沿BD折起到△PBD的位置,使PC=PD,连接PC,得到三棱锥P-BCD,若该三棱锥的所有顶点都在同一球面上,则该球的表面积是( )
如图,在△ABC中,AB=BC=$\sqrt{6}$,∠ABC=90°,点D为AC的中点,将△ABD沿BD折起到△PBD的位置,使PC=PD,连接PC,得到三棱锥P-BCD,若该三棱锥的所有顶点都在同一球面上,则该球的表面积是( )| A. | π | B. | 3π | C. | 5π | D. | 7π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某校在一次高三年级“诊断性”测试后,对该年级的500名考生的成绩进行统计分析,成绩的频率分布表及频率分布直方图如图所示,规定成绩不小于130分为优秀.
某校在一次高三年级“诊断性”测试后,对该年级的500名考生的成绩进行统计分析,成绩的频率分布表及频率分布直方图如图所示,规定成绩不小于130分为优秀.| 区间 | 人数 |
| [115,120) | 25 |
| [120,125) | a |
| [125,130) | 175 |
| [130,135) | 150 |
| [135,140) | b |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6051 | B. | 4034 | C. | 2017 | D. | 1009 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
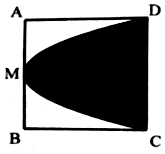 如图,在边长为2的正方形ABCD中,M是AB的中点,则过C,M,D三点的抛物线与CD围成阴影部分的面积是( )
如图,在边长为2的正方形ABCD中,M是AB的中点,则过C,M,D三点的抛物线与CD围成阴影部分的面积是( )| A. | $\frac{2}{3}$ | B. | $\frac{4}{3}$ | C. | $\frac{5}{2}$ | D. | $\frac{8}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com